Computer Graphics (CS4300) 2011F: Exam 1 Example Problems
Exam 1 covers all material from lecture 1 through interpolating polynomials in lecture 13.
- What are you allowed to bring to Exam 1?
- What is a scan line?
- My powerpoint slides end with 2001. What important advances have happened since then?
- What is the width and height of each of the rectangles drawn by these commands?
g2.fillRect(10, 50, 100, 200);
g2.fillRect(30, 70, 100, 200);
What are the coordinates of their corners?
- If wd = 600 and ht = 400, is there any difference between the lines drawn by these two calls?
g2.drawLine(200, 80, 600, 0);
g2.drawLine(wd/3, ht/5, wd, 0);
- How can you use calls to Arc2D to draw and image like this?
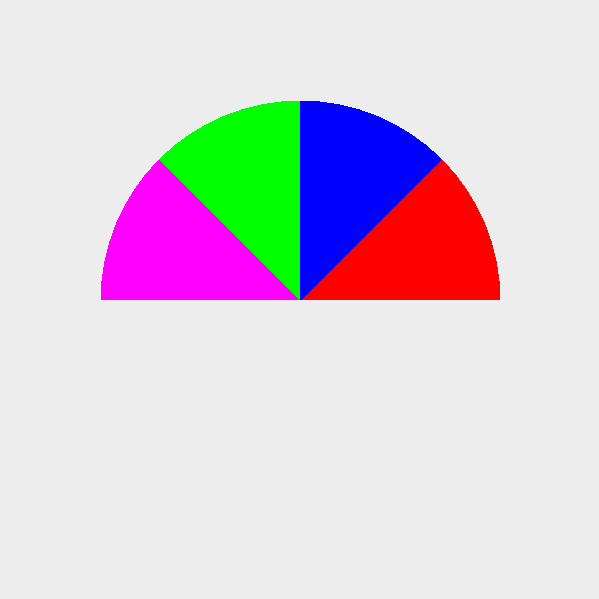
-
Add comments to this code explaining:
- What is the "fly" array for?"
- What do each of the segments numbered 1 through 7 do?
- When the window is first opened, it is 400 by 400 pixels. What is the initial range of values for the coordinates on the random points in section 1?
- What is the difference between GL_TRIANGLE_FAN and GL_TRIANGLE_STRIP in section 5?
- What happens to each of these pieces when you resize the window?
- What is the effect of the glEdgeFlag values GL_TRUE and GL-FALSE?
- What happens when you resize the window?
- The RGB color space can be thought of as an axis-aligned cube in a 3D Cartesian coordinate frame, with one corner at the origin
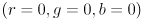 , and the diagonally opposing corner at
, and the diagonally opposing corner at 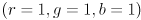 . Every point inside (or on the surface of) this cube corresponds to a particular composite color. Describe the colors encountered when traversing the line segment through the cube from
. Every point inside (or on the surface of) this cube corresponds to a particular composite color. Describe the colors encountered when traversing the line segment through the cube from 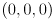 to
to 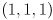 . Draw a diagram of this line segment and describe the approximate color at at least four points on it.
. Draw a diagram of this line segment and describe the approximate color at at least four points on it.
- Give one reason why alternative color spaces, such as HSV (Hue, Saturation, and Value) are useful.
-
For each of the following rgb triples,
(0.0, 0.0, 0.5), (0.5, 0.5, 0.5), (0.2, 0.5, 0.7), (1.0, 0, 0)
show how you might change the rgb values (if possible) to
- Make it darker (An artist might add black paint.)
- Make it paler (An artist might add white paint.)
- Make it more red (An artist might add red paint.)
- Make it as saturated as possible, without changing the hue
- Make it as bright as possible, without changing the hue
- Review of Vectors
- draw a 2D Cartesian coordinate frame and plot two points
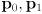 such that
such that 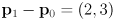
- what conditions must be satisfied by two vectors
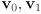 such that you can add them? compute their dot product?
such that you can add them? compute their dot product?
- if
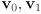 are two
are two 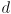 -dimensional vectors, what type of object is the result of
-dimensional vectors, what type of object is the result of 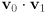 ?
?
- give the result of subtracting the vector
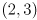 from the vector
from the vector 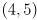
- give a formula for the magnitude
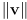 of a vector
of a vector 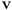 of arbitrary dimension
of arbitrary dimension 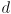
- give a formula to convert any given vector
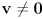 into a parallel unit vector
into a parallel unit vector 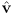 (you may assume that
(you may assume that 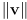 is a function that gives the length of
is a function that gives the length of 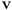 )
)
- given a 2D vector
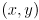 , explain how its direction can be represented as an angle
, explain how its direction can be represented as an angle 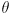 and give a formula for
and give a formula for 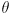 in terms of
in terms of 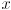 and
and 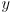
- give a formula for constructing a 2D unit vector
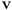 such that the counterclockwise angle between
such that the counterclockwise angle between 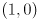 and
and 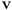 is
is 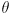 radians
radians
- give the result of multiplying the vector
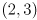 by the scalar 4
by the scalar 4
- is it always true that for two vectors
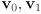 , each of dimension
, each of dimension 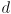 , that
, that 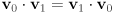 ?
?
- give the result of
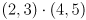
- give a formula for
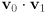 that involves only
that involves only 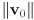 ,
, 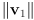 ,
, 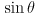 , and
, and 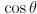 , where
, where 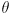 is the angle in radians from
is the angle in radians from 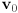 to
to 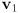
-
Line Segments, Rays, Lines
- define the terms point, ray, segment, and line
- what are the coordinates of the standard basis vectors for a 2D Cartesian frame
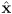 and
and 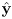 ?
?
- explain how a pair of 2D vectors
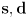 can be used to represent a line segment, a ray, or a line (explain each of the three cases separately; you may call
can be used to represent a line segment, a ray, or a line (explain each of the three cases separately; you may call 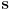 the “start point” and
the “start point” and 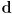 the “direction vector”)
the “direction vector”)
- Working in 2D, let
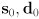 represent an object that is either a segment, a ray, or a line, and let
represent an object that is either a segment, a ray, or a line, and let 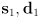 represent another segment, ray, or line. In each case,
represent another segment, ray, or line. In each case, 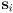 is a point on object
is a point on object  and
and 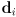 is a vector along the object. For the case of a segment, the object can be said to “start” at
is a vector along the object. For the case of a segment, the object can be said to “start” at 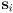 and “end” at
and “end” at 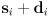 . Assume the objects are not parallel. Set up a single vector equation in two scalar unknowns
. Assume the objects are not parallel. Set up a single vector equation in two scalar unknowns 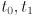 such that the solution can be used to determine if the two objects intersect, and if so, to compute the coordinates of the intersection point. Give the conditions on the values of
such that the solution can be used to determine if the two objects intersect, and if so, to compute the coordinates of the intersection point. Give the conditions on the values of 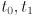 that determine if the two objects intersect when both are considered to be line segments and, separately, when both are considered to be rays. Assuming the objects intersect, give a formula for the location of the intersection point in terms of
that determine if the two objects intersect when both are considered to be line segments and, separately, when both are considered to be rays. Assuming the objects intersect, give a formula for the location of the intersection point in terms of 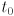 .
.
- draw a 2D Cartesian coordinate frame and plot the line with unit normal
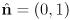 and perpendicular distance 4 from the origin
and perpendicular distance 4 from the origin
- given the unit normal
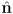 of a line in 2D and its perpendicular distance
of a line in 2D and its perpendicular distance 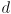 from the origin, show how to use the dot product to form a single vector equation that must hold for all and only points
from the origin, show how to use the dot product to form a single vector equation that must hold for all and only points 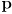 that fall on the line
that fall on the line
- given the unit normal
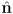 of a line in 2D and its perpendicular distance
of a line in 2D and its perpendicular distance 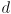 from the origin, show how to use the dot product to form a single vector expression that gives the signed perpendicular Euclidean distance from any point
from the origin, show how to use the dot product to form a single vector expression that gives the signed perpendicular Euclidean distance from any point 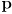 to the line
to the line
- explain how the left hand side of the implicit equation
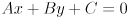 for a line in 2D can be used to define the “left” and “right” sides of the line
for a line in 2D can be used to define the “left” and “right” sides of the line
- given a 2D line segment from point
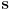 to point
to point 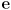 ; (1) give an expression for the vector
; (1) give an expression for the vector 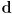 from
from 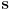 to
to 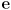 ; (2) give an expression for a vector
; (2) give an expression for a vector 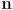 perpendicular to the line (this expression may use the vector
perpendicular to the line (this expression may use the vector 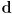 from part 1)
from part 1)
-
Rasters
- draw a picture of the memory layout of a typical greyscale raster with 2 rows and 3 columns (assume the first memory index is in the upper left corner of the raster, and that one byte is used to represent the gray level of each pixel)
- assuming a one byte-per-pixel greyscale raster with
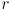 rows and
rows and 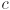 columns stored contiguously in memory starting at the upper left corner, proceeding across the top row, then from left to right across the second row, etc, and ending at the lower right corner, give an expression for the index of the byte corresponding to the pixel at row
columns stored contiguously in memory starting at the upper left corner, proceeding across the top row, then from left to right across the second row, etc, and ending at the lower right corner, give an expression for the index of the byte corresponding to the pixel at row  and column
and column 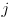 relative to the start of the raster
relative to the start of the raster
-
Midpoint Line algorithm
- What are the inputs to the midpoint algorithm for drawing line segments in 2D? What are the outputs? What is its asymptotic running time as a function of the inputs in “big-O” notation?
- given particular start and end points
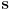 and
and 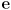 of a 2D line segment in pixel coordinates, draw a pixel grid, and draw the pixels that would be turned on by the midpoint algorithm to rasterize the segment (you may assume that the segment is in quadrant 1 with
of a 2D line segment in pixel coordinates, draw a pixel grid, and draw the pixels that would be turned on by the midpoint algorithm to rasterize the segment (you may assume that the segment is in quadrant 1 with 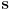 to the left of
to the left of 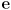 , and that it has more run than rise)
, and that it has more run than rise)
- what exactly is the “midpoint” used in the midpoint algorithm for rasterizing line segments?
- The midpoint algorithm requires checking if a point is above or below the line through two given points
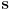 and
and 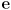 . Give one mathematical way to determine the answer to this question for any given point
. Give one mathematical way to determine the answer to this question for any given point 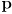 (you may assume that all points are given in pixel coordinates, that the segment is in quadrant 1 with
(you may assume that all points are given in pixel coordinates, that the segment is in quadrant 1 with 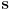 to the left of
to the left of 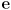 , and that it has more run than rise)
, and that it has more run than rise)
- Zooming in on a line segment in 2D, we might define its “ideal” shape to be a rectangle
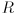 . The width of
. The width of 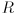 is the desired stroke width and the length of
is the desired stroke width and the length of 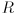 is the length of the segment. Given
is the length of the segment. Given 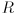 , state a simple algorithm which uses the concept of sampling to determine which pixels should be turned on to approximate the shape. You do not need to show any math, just state in words what the algorithm should do. Do not worry about efficiency. Finally, explain how applying this algorithm to rasterize the segment into a pixel grid with twice the resolution of the screen can be used to draw the line with greyscale antialiasing, by setting each pixel either to 0 (full off), 1 (full on), or grey level
, state a simple algorithm which uses the concept of sampling to determine which pixels should be turned on to approximate the shape. You do not need to show any math, just state in words what the algorithm should do. Do not worry about efficiency. Finally, explain how applying this algorithm to rasterize the segment into a pixel grid with twice the resolution of the screen can be used to draw the line with greyscale antialiasing, by setting each pixel either to 0 (full off), 1 (full on), or grey level 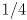 ,
, 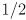 , or
, or 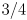 .
.
- give a formula to compute the color
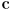 of a pixel that is the result of compositing a foreground color
of a pixel that is the result of compositing a foreground color 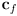 with a background color
with a background color 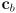 with transparency linearly interpolated by the parameter
with transparency linearly interpolated by the parameter 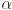 from
from 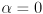 (
(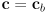 ) to
) to 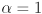 (
(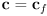 )
)
- describe the types of images that are best compressed with JPEG vs PNG compression and vice-versa
- label the components in a screenshot of a GUI application showing a top-level window with title bar, border, resize handles, window buttons (minimize, maximize, close), menu bar, toolbar, statusbar, scrollbars, child windows, radio buttons, checkboxes, sliders, combo boxes, and tooltips
- explain why it is usually a bad design choice to do time consuming things (like wait for a large download to complete) inside of a single call to a GUI event handler
- define at least five typical mouse-related events that are delivered to GUI applications
- explain how it is possible to receive a “mouse dragged” (i.e. the mouse moved while one of its buttons was pressed) event without first getting a “mouse pressed” event
- explain how it is possible to receive a “mouse pressed” event with no matching “mouse released”, even though the user has released the mouse button and your program is still running
- explain how it is possible to receive a “mouse released” event with out first receiving a corresponding “mouse pressed” event
- You are writing a simple drawing program which allows the user to translate graphical objects by dragging them. You already have a list called “geoms” with the existing objects. Code already exists so that each object can be asked to move itself by a translation vector
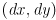 relative to its current position. Similarly, code already exists so that each object can be asked if it contains a given point
relative to its current position. Similarly, code already exists so that each object can be asked if it contains a given point 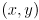 (all coordinates are given in pixels). Write pseudocode for “mouse-pressed”, “mouse-moved”, “mouse-released”, and “mouse-exited” events that implements the drag functionality. You may assume that the mouse only has one button, and that every event receives the current mouse location as parameters
(all coordinates are given in pixels). Write pseudocode for “mouse-pressed”, “mouse-moved”, “mouse-released”, and “mouse-exited” events that implements the drag functionality. You may assume that the mouse only has one button, and that every event receives the current mouse location as parameters 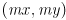 . You may define and use global variables as necessary. Make sure to handle the case where the drag ends but no “mouse-released” event is received by your program.
. You may define and use global variables as necessary. Make sure to handle the case where the drag ends but no “mouse-released” event is received by your program.
-
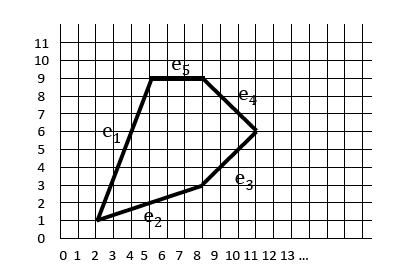
- Given the polygon in the diagram to the right: Create an Edge Table for the polygon (after preprocessing). Show the name and data box for each edge. Label the fields for one edge box.
- Starting with the lowest scanline and working up, show which edges are in the Current Scanline Buffer (Active Edge Table) at each level. Show the data box for each edge at each level where it is active.
- Given a non-degenerate triangle in 2D with vertices
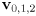 in CCW order, define a barycentric frame by giving its origin
in CCW order, define a barycentric frame by giving its origin 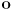 and basis vectors
and basis vectors 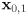 , all in terms of the triangle vertices. Any point
, all in terms of the triangle vertices. Any point 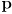 in the plane can now be expressed with two scalars
in the plane can now be expressed with two scalars 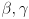 such that
such that 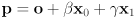 . Draw a triangle, label the vertices
. Draw a triangle, label the vertices 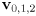 in CCW order, label the point
in CCW order, label the point 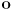 and the vectors
and the vectors 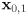 , draw any point
, draw any point 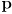 , and estimate the corresponding
, and estimate the corresponding 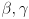 .
.
- Given a picture of a triangle with the lines
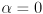 ,
, 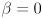 , and
, and 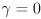 drawn in barycentric coordinates, sketch in the six additional lines
drawn in barycentric coordinates, sketch in the six additional lines 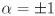 ,
, 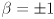 ,
, 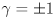 .
.
- Given a non-degenerate triangle in 2D with vertices
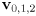 in CCW order, any point
in CCW order, any point 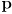 in the plane can be expressed by giving two scalars
in the plane can be expressed by giving two scalars 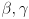 such that
such that 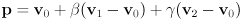 . Give an expression for a third scalar
. Give an expression for a third scalar 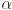 (in terms of
(in terms of 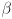 and
and 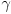 ) such that it is also true that
) such that it is also true that 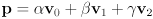 . Then give the mathematical constraints that are satisfied on
. Then give the mathematical constraints that are satisfied on 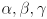 iff
iff 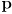 is inside (or on the boundary of) the triangle.
is inside (or on the boundary of) the triangle.
- Given a triangle in 2D with vertices
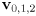 in CCW order and corresponding colors
in CCW order and corresponding colors 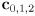 assigned to each vertex, give the formula for barycentric interpolation of a color
assigned to each vertex, give the formula for barycentric interpolation of a color 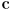 at a point
at a point 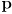 inside the triangle with barycentric coordinates
inside the triangle with barycentric coordinates 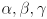 .
.
- Given a triangle in 2D with vertices
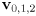 in CCW order and corresponding colors
in CCW order and corresponding colors 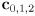 assigned to each vertex, write pseudocode for a simple algorithm to rasterize the triangle using barycentric interpolation to determine the color of all pixels inside (or on the boundary of) the triangle. Do not worry about efficiency. You may assume a function already exists that computes the barycentric coordinates
assigned to each vertex, write pseudocode for a simple algorithm to rasterize the triangle using barycentric interpolation to determine the color of all pixels inside (or on the boundary of) the triangle. Do not worry about efficiency. You may assume a function already exists that computes the barycentric coordinates 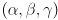 of any pixel
of any pixel 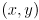 .
.
- define the terms scalar, vector, and matrix
- if
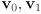 are two
are two 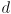 -dimensional vectors, what type of object is the result of
-dimensional vectors, what type of object is the result of 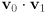 ?
?
- if
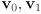 are two
are two 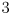 -dimensional vectors, what type of object is the result of
-dimensional vectors, what type of object is the result of 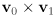 ?
?
- give a formula for the magnitude
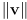 of a vector
of a vector 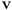 of arbitrary dimension
of arbitrary dimension 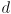
- give a formula to convert any given vector
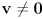 into a parallel unit vector
into a parallel unit vector 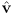 (you may assume that
(you may assume that 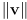 is a function that gives the length of
is a function that gives the length of 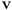 )
)
- is it always true that for two vectors
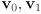 , each of dimension
, each of dimension 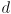 , that
, that 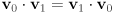 ?
?
- give the result of
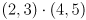
- give the result of
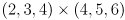
- assume two three dimensional vectors
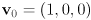 and
and 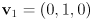 are drawn on a flat sheet of paper; what direction in space would the vector
are drawn on a flat sheet of paper; what direction in space would the vector 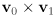 have? what would its magnitude be? What about
have? what would its magnitude be? What about 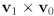 ?
?
- give a formula for
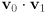 that involves only
that involves only 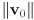 ,
, 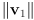 ,
, 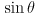 , and
, and 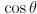 , where
, where 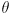 is the angle in radians from
is the angle in radians from 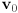 to
to 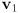
- assuming
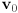 and
and 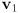 are two 3-dimensional vectors, give a formula for
are two 3-dimensional vectors, give a formula for 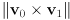 that involves only
that involves only 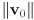 ,
, 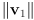 ,
, 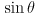 , and
, and 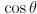 , where
, where 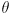 is the angle in radians from
is the angle in radians from 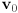 to
to 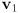
- Let
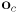 be the origin and
be the origin and 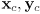 the basis vectors for a 2D child frame defined with respect to a parent frame. Then the equation
the basis vectors for a 2D child frame defined with respect to a parent frame. Then the equation 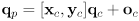 is a transformation from child frame coordinates
is a transformation from child frame coordinates 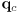 to parent frame coordinates
to parent frame coordinates 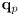 . What condition must hold on
. What condition must hold on 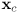 and
and 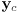 for this to be a rigid transformation?
for this to be a rigid transformation?
- Given the coordinates of the origin
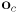 and the basis vectors
and the basis vectors 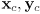 of a 2D child frame defined with respect to a parent frame, and a simple picture drawn with respect to its own coordinate frame, make a drawing of the parent frame, label
of a 2D child frame defined with respect to a parent frame, and a simple picture drawn with respect to its own coordinate frame, make a drawing of the parent frame, label 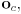
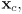 and
and 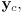 and sketch the picture as it would appear when transformed into the given child frame.
and sketch the picture as it would appear when transformed into the given child frame.
- Show the result of transforming the point
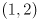 by the matrix
by the matrix 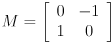 . Is this a rotation, scale, or reflection transformation? If it is a rotation or scale, give the numeric amount(s) by which the transformation rotates (counterclockwise) or scales points. If it is a reflection, identify the axis about which the reflection is taken.
. Is this a rotation, scale, or reflection transformation? If it is a rotation or scale, give the numeric amount(s) by which the transformation rotates (counterclockwise) or scales points. If it is a reflection, identify the axis about which the reflection is taken.
- Same as above with
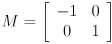 .
.
- Same as above with
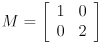 .
.
- If
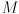 is a
is a 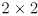 rotation matrix, give a simple operation for computing
rotation matrix, give a simple operation for computing 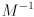 .
.
- Show the result of transforming the point
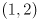 by the homogeneous transformation matrix
by the homogeneous transformation matrix 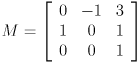 .
.
- Let
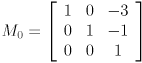 ,
, 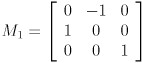 , and
, and 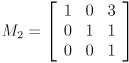 be homogeneous transformation matrices. Show the result of transforming the point
be homogeneous transformation matrices. Show the result of transforming the point 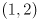 by
by 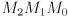 .
.
- Let
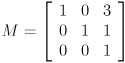 be a homogeneous transformation matrix. Give
be a homogeneous transformation matrix. Give 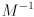 .
.
- Let
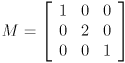 be a homogeneous transformation matrix. Give
be a homogeneous transformation matrix. Give 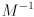 .
.
- Let
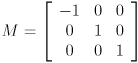 be a homogeneous transformation matrix. Give
be a homogeneous transformation matrix. Give 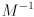 .
.
- Let
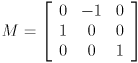 be a homogeneous transformation matrix. Give
be a homogeneous transformation matrix. Give 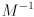 .
.
- If
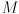 is a
is a 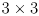 homogeneous transformation matrix corresponding to a pure rotation, give a simple operation for computing
homogeneous transformation matrix corresponding to a pure rotation, give a simple operation for computing 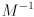 .
.
- Give an informal definition of a “curve.”
- Given the start point
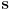 and end point
and end point 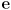 of a line segment, give a vector function
of a line segment, give a vector function 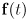 that defines the segment as a parametric curve with
that defines the segment as a parametric curve with 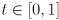 .
.
- Given the start point
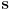 and direction vector
and direction vector 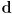 of a ray, give a vector function
of a ray, give a vector function 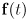 that defines the ray as a parametric curve with
that defines the ray as a parametric curve with 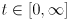 .
.
- Give a vector function
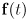 and domain
and domain 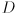 for
for 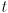 which define a circle with center
which define a circle with center 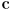 and radius
and radius 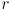 as a parametric curve.
as a parametric curve.
- Give one reason an implicit form for a curve is sometimes preferable to a parametric form.
- Give an implicit form for the line with unit normal
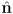 and perpendicular distance
and perpendicular distance 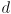 from the origin.
from the origin.
- If
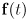 is a vector function for a parametric curve, what related vector function gives the tangent vector
is a vector function for a parametric curve, what related vector function gives the tangent vector 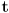 to the curve at
to the curve at 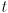 ? And what related vector function gives the normal vector
? And what related vector function gives the normal vector 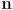 to the curve at
to the curve at 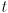 ? Draw any non-straight curve and sketch in
? Draw any non-straight curve and sketch in 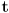 and
and 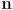 at at least two points on the curve.
at at least two points on the curve.
- Sketch an open curve and a closed curve.
- Sketch a curve which has
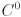 continuity and one which does not.
continuity and one which does not.
- Same as above for
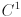 continuity.
continuity.
- Same as above for
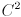 continuity.
continuity.
Last Updated:
Harriet Fell
College of Computer Science, Northeastern University
360 Huntington Avenue #WVH-446,
Boston, MA 02115
Phone: (617) 373-2198 / Fax: (617) 373-5121
The URL for this document is: http://www.ccs.neu.edu/home/fell/CS4300/example-problems/example-problems-E1-Fall2011.html



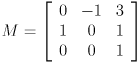 .
.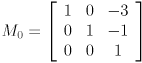 ,
, 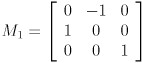 , and
, and 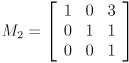 be homogeneous transformation matrices. Show the result of transforming the point
be homogeneous transformation matrices. Show the result of transforming the point 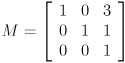 be a homogeneous transformation matrix. Give
be a homogeneous transformation matrix. Give 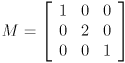 be a homogeneous transformation matrix. Give
be a homogeneous transformation matrix. Give 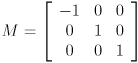 be a homogeneous transformation matrix. Give
be a homogeneous transformation matrix. Give 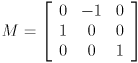 be a homogeneous transformation matrix. Give
be a homogeneous transformation matrix. Give