CS6140 Machine Learning

HW2A - Logistic Regression, SVM, Kernels, Duality

Make sure you check the syllabus for the due date. Please use the notations adopted in class, even if the problem is stated in the book using a different notation.

Make sure to read the notes on Gradient Descent for Regression, and chapter 5 of DHS, up to (including 5.6 Relaxation Procedures)

PROBLEM 1 [30 points]

A) Train/test L2-reg Linear Regression using Gradient Descent (and then test) on Spambase and Housing datasets form HW1.

B) Train/test Gradient Descent Logistic Regression on Spambase data.

Note: Normalization matters. When you normalize data features (one feature at a time), you need to normalize all data (train, test, validation) together, as opposed to normalize separately training and testing sets.

Compare for each dataset training and testing performance across all four learning algorithms by making a table like below

	SVM	Linear Regression (Normal Equations)	Linear Ridge Regression (Normal Equations)	Linear Regression(Gradient Descent)	LogisticRegression(Gradient Descent)
Spambase	Train ACC: Test ACC:	Train ACC: Test ACC:	Train ACC: Test ACC:	Train ACC: Test ACC:	Train ACC: Test ACC:
Housing	Train MSE: Test MSE:	Train MSE: Test MSE:	Train MSE: Test MSE:	Train MSE: Test MSE:	N/A . - WHY?

For classification (Spambase), produce Confusion Matrices (TruePos, FalsePos, TrueNeg, FalseNeg) for Decision Trees, Linear Regression and Logistic Regression - three 2x2 matrices. You will have to use a fixed threshold for each regression algorithm.
For classification (Spambase), produce ROC plots comparison between linear regression and logistic regression - two curves. Compute the AUC for each curve.

PROBLEM 2 [30 points, GR_ONLY]

Run Logistic Regression on the Spambase dataset, but using Newton's numerical method instead of Gradient Descent. An intro to Newton's method can be found in the lecture notes.

PROBLEM 3 SVM library [40 points]

A) Run an SVM from a package or library of your choice on the Spambase dataset. Try several kernels, including the polynomial and the RBF ones. Report the results. Use the SVM package of your choice, for example one of these: SVMlight, SGDSVM, osu SVM, LIBSVM, Matlab SVMtrain, or other software (here, here).

B) Run an SVM from a package or library of your choice on the Digits Dataset (Training data, labels. Testing data, labels; you can extract features on your own). Alternatively you can use extracted HAAR features . If you choose an SVM package that does not provide multi-class implementations, you should write a wrapper that will make the code run for each class versus the others, separately.

PROBLEM 4 [30 points] Implement your own SVM with SMO solver for Spambase

Instead of using a SVM package, implement your own using SMO optimization with linear kernel, and run on Spambase dataset (split 80% train - 20% test). Compare with Problem 1 results. Here is an SMO article, and a SMO simplified version .

[optional] use the RBF kernel instead, with your SVM-SMO implementation.

PROBLEM 5 [30 points] k-Nearest Neighbors (kNN)

Implement the kNN classification algorithm such that it can work with different distance functions (or kernels as similarities)

A ) Fix values of ‘k’= "the number of closest neighbors used", i.e. k=1,k=3, and k=7.

Spambase dataset. Try k=1,3,7 with Euclidian distance.

Digits Dataset, with extracted features. Try k=1,3,7 and the following similarities/distances: Cosine distance, Gaussian Kernel, Polynomial degree-2 Kernel

B ) Fixed Window. Instead of using the closest k Neighbors, now we are going to use all neighbors within a window. It should be clear that a testpoint z₁ might have many neighbors (a dense area) in its window, while another testpoint z₂ might have only (a sparse area) or none at all.
Fix an appropriate window size around the test datapoint by defining a windows "radius" R , or the maximum distance allowed. Predict the label as the majority or average of training neighbors within the window.

Run on Spambase dataset with Euclidian distance.
Run on Digits dataset with cosine distance.

C) Kernel density estimation. Separately for each label class, estimate P(z|C) using the density estimator given by the kernel K restricted to the training points form class C. There is no need for physical windows, as the kernel is weighting each point by similarity:

where m_C is the number of points in the training set with label C. Then predict the class by largest Bayesian probabilities P(C|z) = P(C) * P(z|C) /P(z).

Run on Spambase dataset with Gaussian kernel.
(optional) Run on Digits dataset with Gaussian kernel
(optional) Run on Digits dataset with polynomial kernel.

PROBLEM 6 [30 points ] Kernel Ridge Regression on Simple Non Linear Data

Load the WAVE dataset ( X coordinates and Y coordinates ) and the CRESCENT dataset ( X coordinates and Y coordinates ). Split into train and test 80-20 (package allowed).
A) Implement a wrapper for kernel ridge regression. The wrapper can be designed functionally or object-oriented, but it should include a fit(X, y) function, and a predict(X) function. The initialization of the wrapper should include the type of kernel (linear, polynomial, and RBF) as well as the associated hyperparameters for each kernel. The kernel itself can be implemented with a package, but everything else must be done from scratch.
B) Use your kernel ridge regression implementation to fit the wave X-coordinates to the circle Y-coordinates, trying out Linear, RBF and polynomial kernels. You will need to tune the hyperparameters for each kernel to get the best results
C) For each kernel, evaluate the fitted kernel ridge regressor on both the train and test sets via MSE loss, and plot the true circle X coordinates against the predicted circle Y coordinates (colored red), over the true circle X coordinates against the true circle Y coordinates (colored blue).
D) Repeat steps b and c for the crescent dataset
E) Explain which kernels did better for each dataset, and give a hypothesis why

PROBLEM 7 Implement your own SVM with SMO solver for Digit Dataset [optional, no credit ]

Instead of using a SVM package, implement your own using SMO optimization and run it on the Digits Dataset (Training data, labels. Testing data, labels) with HAAR features extracted on HW5. Compare with Problem 1 results. The Digits dataset is very learnable, so to speed up the computation you can sample the training set at 10% or 20% per class (but make sure to use the entire testing set for measuring performance).
If you did not extract HAAR Features for previous HW, you can use our version of MNIST_HAAR_dataset
Since the data has a range of 10 labels (multiclass) while your SVM is a binary classifier, you will have to implement a wrapper on top of the SVM. You can choose one of the following:

One-vs-the rest approach and train 10 SVM classifiers (one per class)

Run ECOC on top of SVMs (similar with HW5 setup, only with SVM instead of boosting)

We suggest a voting schema: train all possible one-to-one SVM classifiers, for a total of (10 choose 2) = 45 models. Each one of these will train/test only on labeled data for the two particular classes is made for : for example 7vs9 SVM will only train/test on datapoints labeled 7 or 9. To obtain a multiclass classifier: first run (for a given test-datapoint) all 45 models and get their scores; then you would need a voting strategy in order to decide a prediction or a ranking among all 10 classes. Such voting strategy can be to predict the class with most wins, and if there is tie for the most wins to use the direct "match" one-to-one to break the tie.

PROBLEM 8 [optional, no credit ]

Explain why 0 $\leq$ $α$ $\leq C/m$ is a constraint in the dual optimization with slack variables. (HINT: read Chris Burges tutorial first) Distinguish three cases, and explain them in terms of the classification and constraints: a) 0 $=$ $α$ ; b) 0 $<$ $α$ < C/m; c) $α$ $=
C/m.$

$This has
been discussed in class and in SVM notes; a detailed rigurous
explanation is expected.$

PROBLEM 9 [optional, no credit]

Consider the following 6 points in 2D, for two classes:

class 0: (1,1) (2,2) (2,0)

class 1: (0,0) (1,0) (0,1)

a) Plot these 6 points, construct the optimal hyperplane by inspection and intuition (give the W,b) and calculate the margin.

b) Which points are support vectors ?

c) [Extra Credit] Construct the hyperplane by solving the dual optimization problem using the Lagrangian. Compare with part (a).

PROBLEM 10 Implement better SMO [optional, no credit]

Extra points will be given for an SMO implementation for both PB2 and PB3 that is reasonable fast.
Extra points will be given for an implementation for both PB2 and PB3 that works with kernels (for example Gaussian Kernel)

PROBLEM 11 [optional, no credit]

Run your SMO-SVM on other datasets.

PROBLEM 12 [optional, no credit]

Same problem as 2, but dont use SMO. Instead use a built in (or existing library) quadratic solver from Matlab, Python, Java, C etc, inn order to solve the dual problem.

PROBLEM 13 [optional, no credit]

What is the VC dimension of the SVM with linear kernel ?

PROBLEM 14 [optional, no credit]

DHS chapter 5 Pb 2 (page 271)

PROBLEM 15 [optional, no credit]

DHS chapter 5 Pb 5, page 271

PROBLEM 16 [optional, no credit]

DHS chapter 5 Pb 6, page 271

PROBLEM 17 [optional, no credit]]

For a function f(x1,x2,..., xn) with real values, the "Hessian" is the matrix of partial second derivatives

Consider the log-likelihood function for logistic regression

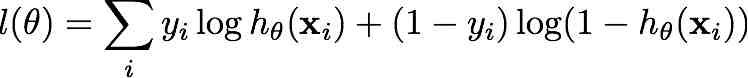
Show that its Hessian matrix H is negative semidefinite, i.e. for any vector z satisfies

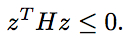
Remark: This fact is sometimes written $H \leq 0$ and implies the log-likelihood function is concave.

Hint: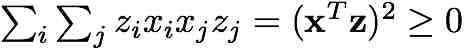