CSU390 08S: Homework 04

Assigned: Thu 07 Feb 2008
Due: Thu 14 Feb 2008

General Instructions

1. Please review the grading policy outlined in the course information page.

2. On the first page of each part of your solution write-up, you must make explicit which problems are to be graded for "regular credit", which problems are to be graded for "extra credit", and which problems you did not attempt. Please use a table something like the following

   Problem	01	02	03	04	05	06	07	08	09	...
   Credit	RC	RC	RC	EC	RC	RC	NA	RC	RC	...

   where "RC" is "regular credit", "EC" is "extra credit", and "NA" is "not applicable" (not attempted). Failure to do so will result in an arbitrary set of problems being graded for regular credit, no problems being graded for extra credit, and a five percent penalty assessment.

3. You must also write down with whom you worked on the assignment. If this changes from problem to problem, then you should write down this information separately with each problem.

Specific Instructions

1. For each part of Problem 1 below, you should either prove that the assertion is true (by appealing to closure properties) or demonstrate that it is false by providing a counterexample.

2. For Problems 2 through 6, you should use the Pumping Lemma and/or appeal to closure properties. For examples of complete and correct Pumping Lemma proofs, see Examples 1.73, 1.74, 1.75, 1.76, and 1.77 on pages 80-82 of the Sipser text.

   The use of closure properties may also be helpful and may, in fact, yield complete proofs without the need to resort to the Pumping Lemma (as discussed in class).

   For examples of proofs for non-regularity via closure properties and the Pumping Lemma, please see the following linked handout.

Problems

Required: 5 of the following 6 problems
Points: 20 pts per problem

1. Given any two sets A and B, the set difference A-B is constructed by removing the elements in B from A. For example, if A = {1, 2, 3, 4, 5} and B = {2, 4, 6, 8}, then A-B = {1, 3, 5}. In mathematical terms,

   

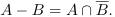
   Let R be any regular language and let N be any non-regular language. (Note: R is not the set of regular languages; it is a variable which represents any particular regular language. Similarly for N.)

   For each of the following assertions, either prove that the assertion is true or demonstrate that it is false by providing a counterexample.

   • R-N is always regular.
   • N-R is always non-regular.

2. Prove that the following languages are non-regular:
   • the language defined in Exercise 1.29 part (b) and
   • {w : every prefix of w has at least as many 0s as 1s}.

3. Prove that the following languages are non-regular:
   • the language defined in Problem 1.46 part (c) and
   • {w : w contains a prime number of 0s and a prime number of 1s}.

4. Problems 1.46 part (d) and 1.49 part (b).

5. Prove that the following languages are non-regular:
   • {0^m1ⁿ0^m+n : m >= 1 and n >= 1} and
   • {0ⁱ1^j0^k : j = max{i,k}}.

6. Prove that the following languages are non-regular:
   • the language defined in Problem 1.35 and
   • {w : w contains twice as many 0s as 1s}.

Switch to:

• Homework 03
• Homework 05