Review for Quiz #2 to be given April 5th

CSU540 Computer Graphics - Spring 2005 - Prof. Futrelle

Posted 2 April 2005

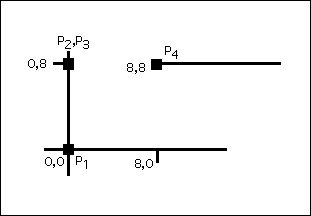
Bézier curves: Here is the type of question you'll see. There may be other more qualitative ones that simply ask you to draw estimated control points for curves or draw a curve that's a good approximation to the one dictated by some control points I will give you.

In the diagram below, a Bézier curve is to be drawn from P₁ to P₄ using control points P₂ and P₃ which are both located at 0,8.

Use the cubic Bézier formula for the curve:

Q(t) = (1 - t)³ P₁ + 3t(1 - t)² P₂ + 3t²(1 - t) P₃ + t³ P₄

and apply it to the following figure. In particular, compute the x,y coordinates of the point on the curve at t = 1/2. By symmetry, this point should lie along the line from 0,8 to 8,0. Does it? Describe the convex hull of the four control points. Is the point you computed within this hull?

Diffuse reflection: You should understand the material on pages 478 through 481. In particular, you should understand and memorize equation 14.5. (Understanding it makes it easy to memorize, needless to say.) You should be able to answer a simple question based on equation 14.5. You should know that each color component, R, G, and B is treated independently of the others. You should know the relation between the dot product and its cosine form, as well as how to normalize a vector.

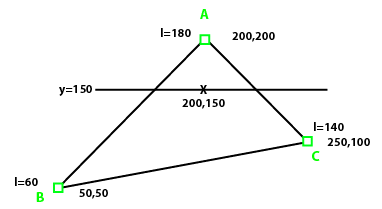
Gouraud shading:

The diagram below illustrates the type of question you will be given. Your task is to figure out the interpolated intensity at the point 200,150 shown. Note that it's not necessary to use the full linear interpolation algebra on page 494. In example below, you can figure out the following, essentially by inspection. The problem on the quiz will be similar.

• On the right, the edge AC, the y scan line is exactly halfway between the A and C y-coordinates. This means that the intensity at the point where the scan line intersects AC is the average of the intensities at A and C or (180 + 140)/2 = 160. (It would help if you labeled that point and the intensity you compute for it.
• On the right, the edge AB, the y scan line divides the y distance by 1/3 to 2/3. Thus, the weighted average of the intensities at A and B is: 2/3 x 180 + 1/3 x 60 = 140.
• The point 200,150 on the scan line is exactly halfway between the two edges. So the intensity should be (160 + 140)/2 = 150. That's the answer.

An extra credit question (10%): Computing the average normal to a common vertex of three triangles based on computing the normal to each of the three triangles using the cross products of a pair of edges. If you understand how to get the edges from the vertex coordinates and how to compute the cross product from the determinant formulation, you will be able to solve this problem.

Go to CSG140 home page. or RPF's Teaching Gateway or homepage