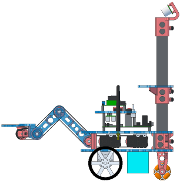
Basic Kinematics and Dynamics of Rotation
- many motions in a robot are ultimately driven by rotation of a shaft
- partly due to engineering convenience
- of course, wheels are a very important case
- in our robot, all motions are driven by shaft rotations — both the wheels and the arm joints
- Kinematics is the study of the geometry of motion without considering what is physically powering the motion
- 360 degrees =
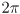 radians = 1 revolution
radians = 1 revolution
- circumference =
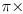 diameter
diameter
- what is robot travel speed in mm/s if wheel rotation speed is 1 rev/s and wheel radius is 50mm? (ans: about 314 mm/s)
- Dynamics is the study of the physics of motion
- force is the product of mass times acceleration:
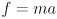
- measured in Newtons:
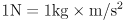
- this is Newton’s second law
- Newton’s first law: things move with constant (possibly zero) velocity unless acted upon by a force, which causes them to accelerate (change velocity)
- (Newton’s third law: an applied force has an equal and opposite reaction force)
- example: a 1kg mass experiences a 9.81 N downward force because the acceleration due to gravity on Earth is
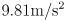
- if force and mass are known, the equation can be easily rearranged to calculate acceleration: a = f/m
- torque = tangential force
 lever arm length (at an instant)
lever arm length (at an instant)
- so if force is measured in Newtons and length in meters, then torque is measured in N
 m (Newton-meters)
m (Newton-meters)
- what is robot propulsion force in Newtons for a wheel with radius 50mm driven with 1N
 m torque? (ans: 1N
m torque? (ans: 1N
 m = f
m = f
 (50mm
(50mm
 (1m/1000mm), so 1N = f/20 or f = 20N)
(1m/1000mm), so 1N = f/20 or f = 20N)
- at what rate will the robot accelerate in this case if it has a mass of 1kg? (ans: 20N/1kg = (20kg
 m/s
m/s
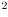 )/1kg = 20m/s
)/1kg = 20m/s
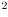 — pretty quickly!)
— pretty quickly!)
- this ignores the work the motor would have to do to make the wheel itself spin (and a lot of other things)
- a reasonable assumption, in many robots the wheels have a relatively low mass compared to the rest of the robot
- if the wheel was very chunky, we might want to use a rotary version of f=ma:
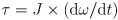 , where
, where
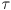 is torque (instead of force), J is the moment of inertia of the wheel (instead of mass), measured in kg
is torque (instead of force), J is the moment of inertia of the wheel (instead of mass), measured in kg
 m
m
 , and
, and
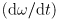 is the rotary acceleration in rad/s
is the rotary acceleration in rad/s
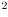
- energy is the integral of force applied over a distance, with units of Joules: 1J = 1N
 m
m
- for a rotating shaft, this is the integral of torque applied over some amount of rotation measured in radians
- measuring in radians has the effect of calculating the circumferential distance over which the tangential force is applied
- power is the (instantaneous) rate of flow of energy measured in Watts: 1W = 1J/s
- for linear motion, power = force
 speed, or W = J/s = (N
speed, or W = J/s = (N
 m)/s = N
m)/s = N
 (m/s)
(m/s)
- for rotary motion with speed measured in radians per second, power = torque
 speed, or W = J/s = (N
speed, or W = J/s = (N
 m)/s = (N
m)/s = (N
 m)
m)
 ([rad]/s) (note, radians are actually “unitless”)
([rad]/s) (note, radians are actually “unitless”)
Actuating Rotation with Electric Motors
- there are a variety of ways to make a shaft rotate, including pneumatics (air power), hydraulics (fluid power), turbines, combustion engines (as in a traditional automobile), etc.
- electric motors are a very common choice in most kinds of robotics
- relatively low cost
- relatively low complexity
- relatively compact
- reasonably efficient
- reasonably strong
- action of a motor is based on the electromagnetic effect: current passing through a coil of wire produces a magnetic field
- the rotating part of the motor — the rotor — may have either coils or permanent magnets
- the motor housing — the stator — also may have either coils or permanent magnets (note that at least one of the rotor and stator must have coils)
- the interaction of the two magnets produces force at some radius, which equals torque
- the shaft begins to rotate
- the current is then switched in the coils in such a way that a torque is always applied to the rotor (commutation)
- Stepper Motors
- perhaps the simplest motor type to understand
- usually the rotor is a radial array of bar magnets
- the stator is a corresponding radial array of coil phases
- the two ends of each coil phase are exposed as motor leads (stepper motors have more than two leads)
- current is sequenced through the phases in logical steps by external electronics — external commutation
- the shaft rotates by a fixed increment for each step
- both forward and reverse rotation are possible
- if the sequence is halted but current remains in the coils, the shaft holds its position
- steppers only operate correctly up to some maximum external load — any higher and steps will be “skipped”, or the motor could even be pushed in reverse
- DC Motors
- stepper motors are common in devices that require mechanical positioning under well-controlled conditions, so that skipped steps are prevented
- many robots are used in varied applications where such guarantees are hard to make
- steppers are also not particularly efficient at producing continuous rotation
- for these reasons, a more common type of motor is called the DC motor
- DC motors have one coil with two exposed leads
- the coil can be either in the rotor or the stator
- the motor is internally commutated, most commonly with an arrangement of brushes and contacts that switch the polarity of current in the coils so that the rotor always experiences a torque pushing it “forward”
- whether “forward” means clockwise or counterclockwise rotation depends on the polarity of the applied voltage
- switch the wires to reverse the motor
- electrically, an arrangment of four switches called an H-bridge is commonly used to gate current in either direction through the motor
- control can be reduced to two binary signals
- the direction signal determines the direction of current flow (and hence the motor torque direction)
- the power signal just turns the motor on or off
- to turn the motor on by a variable amount, another common technique is to use pulse width modulation (PWM)
- the power signal is not left on or off for a long time, but quickly switched at a regular interval, e.g. every 1ms
- the percent of time the signal spends high — determined by the width of the positive pulses — controls the amount of electrical power delivered to the motor
- often MCUs have dedicated on-chip peripherals to generate these kinds of PWM signals, with e.g. 8 bits of resolutoin to set the pulse width
- TBD figure
DC Motor Model (optional)
- the amount of torque produced is often modeled as proportional to the amount of current that is going through the coils:
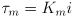 , where
, where
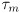 is the motor torque in N
is the motor torque in N
 m,
m,
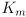 is the torque constant in (N
is the torque constant in (N
 m)/A, and
m)/A, and
 is the current in Amps (A)
is the current in Amps (A)
- recall that for a rotating shaft, power = torque
 speed, or
speed, or
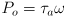 , where
, where
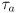 is the applied torque, i.e. the amount of torque that an external load is actually pushing back on the motor
is the applied torque, i.e. the amount of torque that an external load is actually pushing back on the motor
- if
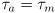 , the motor shaft will not accelerate (its speed will remain constant)
, the motor shaft will not accelerate (its speed will remain constant)
- this rarely happens in practice
- constant speed is instead achieved by regulating and controlling the motor with a higher-level algorithm, with speed monitored by a rotation sensor (more on these topics later)
- if
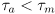 , the shaft will accelerate “forward” (motor drives the load, the normal condition)
, the shaft will accelerate “forward” (motor drives the load, the normal condition)
- if
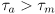 , the shaft will accelerate “backward”
, the shaft will accelerate “backward”
- the actual shaft acceleration can be calculated if the moment of inertia J of the rotor and any connected rotating mass is known:
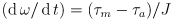
- current flowing through a coil also generates heat due to the resistance of the coil
- heat is a form of power, hence it is measured in Watts
- the law is power = current
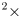 resistance, with current measured in Amps and resistance in Ohms, or
resistance, with current measured in Amps and resistance in Ohms, or
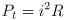
- when a motor is receiving electrical power but the shaft is not moving (e.g. because some external load is holding it fixed), all the incoming power turns into heat
- the temperature of the motor will rise until an equilibrium is reached where the rate of heating equals the rate of heat dissipation
- often that would be a very high temperature, which would damage the motor
- thus care must be taken not to stall a motor for very long, or to limit the incoming current when a motor is stalled
- when a motor is actually spinning, the incoming electrical power turns into both heat and into mechanical output power
- motor efficiency is ratio of input power to useful output power (typically the heat is not considered useful)
- eletrical power, also measured in Watts, is the product of applied voltage and current:
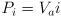
- so efficiency is
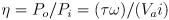
- in reality, a variety of physical and electrical phenomena affect the behavior of the motor
- but to a significant extent we can make a simplified model that only considers
- the applied Voltage
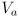 and the electrical current
and the electrical current
 flowing through the motor
flowing through the motor
- the electrical resistance
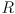 of the motor
of the motor
- the motor torque constant
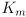
- the moment of inertia
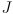 of the motor shaft and whatever may be connected to it
of the motor shaft and whatever may be connected to it
- the torque
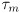 the motor is applying to the load
the motor is applying to the load
- the torque
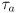 the load is applying to the motor
the load is applying to the motor
- the relation
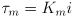
- Newton’s law
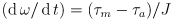
- the rotation speed
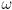
- a back-emf constant
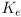
- a back-emf voltage
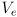
- the relation
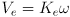
- the back-emf voltage represents the effect that the motor’s own rotation has as a generator — the rotating shaft actually generates a voltage in the coils that is proportional to the rotation speed
- this voltage opposes the applied voltage, which leads to the first of two constituitive equations for the simple motor model:
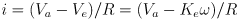
- the second constituitive equation is Newton’s law:
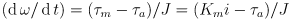
- these equations come into play both when designing motors and their controllers, as well as when selecting a motor suitable for a particular task
- in particular, they can help make graphs of
- velocity and current vs torque — velocity decreases and current increases as torque increases
- TBD figure
- power and efficiency vs torque — efficiency is usually maximized at a relatively low torque, and power is usually maximized at a medium torque
- TBD figure
Rotation Sensors
- in order to rotate at a desired speed or by a desired amount, we will need to actually measure the rotation
- otherwise there are usually too many unknowns to reliably predict the rotation speed or amount
- often we can buy a motor packaged together with a rotation sensor and its own MCU, all in one box — a servo
- will learn more about these when we study robot arms
- a simple and common rotation sensor is a potentiometer (pot)
- a pot is a variable resistor, usually set up in a circuit that acts as a voltage divider
- pots have three wires, one for each end of a fixed internal resistor, and one for a wiper that touches a variable point along that resistor
- the wiper is mechanically connected to the rotating shaft, and the body of the pot to the motor case
- the two ends of the pot’s resistor are typically connected to some positive voltage reference (e.g. 5V) and to ground (0V)
- the wiper voltage then varies, usually linearly, from 0 to 5V as the shaft rotates
- this can be read out and converted to a binary number (typically 8-10 bits) by an analog-to-digital converter, another common type of MCU on-chip peripheral
- one big problem with pots is there is always a dead zone where the wiper is between the two ends of the internal resistor — the voltage, and hence the shaft position, is indeterminate in that zone
- pots also wear down over time, and may have accuracy or linearity problems
- one good feature of pots is that they are absolute in the sense that the shaft angle is known immediately upon power-up
- encoders are an alternative rotation sensor
- usually more expensive than pots, but can resolve all the issues
- a common form of encoder is an incremental quadrature encoder
- a rotating code wheel is attached to the motor shaft, with a regular pattern of light/dark stripes around their perimeter
- two detectors watch the stripes and generate binary data, e.g. when a light stripe is under the dector the output is 1, and 0 for a dark stripe
- the detectors will produce pulse trains as the shaft rotates
- by placing the detectors with a 90 degrees phase shift relative to the pitch of the code wheel, one will switch first when the shaft rotates clockwise, and the other will switch first when it rotates counterclockwise (this is called quadrature readout)
- magnetic (Hall Effect) and other types of sensor can be used instead of optical
- one problem is that this type of encoder is an incremental device — we do not know the starting position of the shaft, only how it has changed since power-up
- one way to resolve the power-up problem is to add a limit switch or index sensor that tells us when the shaft has reached a known position
- at power up, if we can guarantee that it will always be safe to do so, we can just start spinning the shaft until the limit switch or index sensor fires
- from then on we know the shaft position
- another way to resolve the problem is to just not worry about it
- especially for a wheel actuator, this is the most common approach, because wheels are typically rotationally symmetric anyway
- a third way is to use multiple readout sensors that watch concentric circles of stripes on the codewheel — the absolute encoder
- for example, if 8 sensors are used, at any time their output is an 8-bit number that gives the position of the shaft, even right after power-up
- the added hardware and codewheel complexity make absolute encoders more expensive then incremental
- if the usual “binary counting” pattern is used on the codewheel, there is a problem when multiple light/dark edges simultaneously align under the readout sensors
- ideally, they will all switch at the same instant
- but in practice there will be some sequence of switching depending on the vagaries of noise, the manufacture of the codewheel and the sensors, etc
- this will give incorrect positions while the codwheel is near such a transition
- fortunately, there is a simple solution: use a different pattern with
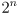 variations where
variations where
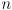 is the number of readout sensors, but in which no two light/dark edges radially align
is the number of readout sensors, but in which no two light/dark edges radially align
- such a pattern exists and is called the Gray code
- this is the standard pattern used on absolute encoders
- a third type of rotation sensor directly uses the Hall effect to sense the orientation of the field of a magnet attached to the shaft
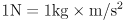
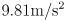
 m (Newton-meters)
m (Newton-meters)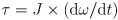 , where
, where
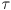 is torque (instead of force), J is the moment of inertia of the wheel (instead of mass), measured in kg
is torque (instead of force), J is the moment of inertia of the wheel (instead of mass), measured in kg
 m
m
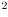 , and
, and
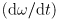 is the rotary acceleration in rad/s
is the rotary acceleration in rad/s
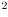
 speed, or W = J/s = (N
speed, or W = J/s = (N
 m)/s = N
m)/s = N
 (m/s)
(m/s) speed, or W = J/s = (N
speed, or W = J/s = (N
 m)/s = (N
m)/s = (N
 m)
m)
 ([rad]/s) (note, radians are actually “unitless”)
([rad]/s) (note, radians are actually “unitless”)