- They do correspond to the physical inversions that occur in a true pinhole camera, and also in many lens-based cameras.
- But in practice the image can be flipped as part of its transfer off the image sensor.
- TBD diagram
- In this model, the pinhole is renamed the center of projection (CoP).
- Typically
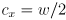 and
and
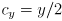 where the image is
where the image is
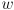 pixels wide and
pixels wide and
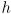 pixels tall. Slight errors in camera manufacturing can make the actual as-built values of
pixels tall. Slight errors in camera manufacturing can make the actual as-built values of
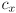 and
and
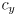 vary (for each specific camera) from this ideal.
vary (for each specific camera) from this ideal.
- The mathematical model can accommodate such cameras by using independent horizontal and vertical focal lengths
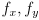 .
. - In the case of non-square pixels, the “length of a pixel” is typically the smaller of the two pixel side-lengths, and
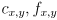 are all measured in units of this length.
are all measured in units of this length.
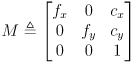
(3)
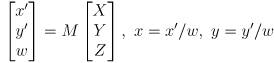
or
- For a known object point
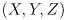 and known corresponding image point
and known corresponding image point
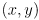 , the projection model (2) can be considered to give two constraints on the four unknown parameters
, the projection model (2) can be considered to give two constraints on the four unknown parameters
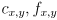 .
. - Thus, it should be theoretically possible to solve for the unknowns given observations of two object points and their corresponding image points.
- It is preferable to use many more pairs to average out any measurement errors.
- In practice we want to find them automatically. There are various ways to do that, but a common approach is to design a calibration object with well-defined corners between light and dark regions. These can be found automatically in the image by methods similar to edge detection.
- Nowadays variations of chessboards are very common calibration objects, partly for this reason.
- You could use a tape measure, but this would be subject to human error, and would be very tedious.
- Perhaps surprisingly, for a calibration object with known geometry—like a specific chessboard pattern—it is possible to simultaneously solve for both the camera intrinsic parameters and the relative pose of the chessboard to the camera.
cvCalibrateCamera2(objectPoints, imagePoints, pointCounts, imageSize, cameraMatrix, distCoeffs, rvecs, tvecs, flags) which assumes a chessboard-style calibration object
objectPoints- coordinates of points on the calibration object relative to a frame on the object (so this is determined by the design of the chessboard pattern)imagePoints, andpointCounts- observed pixel locations corresponding to all the object points, typically for multiple views of the object in different (unknown) posesimageSize- size of the camera image in pixelscameraMatrix- written on output to be the reconstructed camera matrix
camera matrix
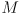 as in equation (3) above, which includes the four intrinsic parameters
as in equation (3) above, which includes the four intrinsic parameters
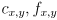
distCoeffs- a vector of four or 5 additional camera intrinsic parameters that are also written on output, more info on them below (the number of coefficients calculated, 4 or 5, is determined by the size of the passed matrix into which they will be stored)rvecs,tvecs- optional paramters, default NULL. If non-null then these are storage space to return the calibration object pose in camera frame for each of the provided views. More info on these below.flags- various options to control the calibration algorithm can be specified here.
- It is not possible by such methods to measure
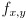 in physical units like meters, or equivalently, to determine the physical size of a pixel.
in physical units like meters, or equivalently, to determine the physical size of a pixel. - This can only be done if the focal length is known in physical units a-priori, or by using a microscope to measure the spacing of pixels on the actual imaging chip.
- For related reasons, some knowledge about the physical shape of an object (such as the chessboard dimensions) is required in order for its pose to be unambiguously recovered by a monocular camera.
- This is true even if the camera can be moved around to observe the object from different viewpoints, unless some information about the geometric relationships of those viewpoints is externally supplied.