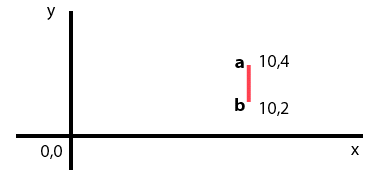
Question 1. For the figure below, transform the endpoints a and b
of the line segment to transform the line segment.
Each transform should be a 3x3 matrix (homogeneous coordinates).
The transforms you are to construct and apply are first: Construct a translation matrix
that moves the center of the line segment to the origin and then apply it to a and b.
Second, rotate each resulting point around the origin by -90° (minus 90 degrees).
Third, transform those resulting endpoints using the inverse of the original translation.
Draw the final state of the line segment, indicating each transformed
endpoint, a' and b'. Explain intuitively why you expect it to appear as you computed.
Question 2. Write out the 2x2 rotation matrix R(φ), for the general angle φ, and
another, R(-φ), for minus φ.
Form the product of R(φ) and R(-φ) and
show that it is the identity matrix.
Question 3. Two planes have [x,y] normal vectors n1 = [1,0]
and n2 = [1,1] (no z component).
Compute the dot product of the two using Cartesian coordinates and show that the result is
equal to the result obtained by using the formulation:
n1·n2 = ||n1|| ||n2|| cosφ.