Introduction to Scheme, Part 1

Preliminary

To participate in this lab you will need to follow some basic first steps:

1. Groups of 2: You need to form teams of two people. Each group will work on a single computer. Both people discuss the exercises and think about the problem in hand; only one of the two types the code. You should switch places with your partner in about the middle of the lab.

2. Log in the machine: Use the ccis login and password of one of the members of your team to log into the computer you are using. You should all have a ccis account by now, but if for some reason both the members of a team don't have an account, you should find a team with two working accounts and switch partners.

3. Run DrScheme: DrScheme will be our working scheme environment for this lab (and later for the CSG111 course). Find DrScheme in the Start menu and run it.

When you do all of the above, you are ready for the lab.

Expressions

Maybe the most fundamental building block in Scheme (and other languages) is an expression. An expression is a piece of syntax that returns one result. An expression can be as simple as a single number

    5

or more complex as the calculation of the square root of a number

    (sqrt 5)

(Don't be alarmed if you don't understand the above syntax just yet.)

You can try typing the above examples in the bottom half (a.k.a. Interaction Window) of DrScheme. There you will see a prompt > and next to it you can type an expression. Whenever you write an expression next to the prompt and press enter, DrScheme will "evaluate" the expression and print the "result" in the line underneath.

    > 5
    5

    > (sqrt 5)
    2.23606797749979

In the next section we will see how we can use the interaction window of DrScheme as an advanced calculator.

Numbers, Booleans, and Arithmetic

As we mentioned above, some of the primitive expressions in Scheme are numbers; positive and negative, integers and decimals

    > 17
    17

    > -10
    -10

    > 3.1415
    3.1415

Scheme also has a set of arithmetic operators that work with numbers.

    ; + : Number * Number --> Number
    ; Adds two numbers and returns the result

    ; - : Number * Number --> Number
    ; Subtracts two numbers and returns the result

    ; * : Number * Number --> Number
    ; Multiplies two numbers and returns the result

    ; / : Number * Number --> Number
    ; Divides two numbers and returns the result

+, -, *, / are the names of the operators.

Number * Number --> Number is the Contract for each of them. It guarantees that these operators take two numbers as arguments and return a number as a result. Knowing the contract of an operator is imperative in order to use it correctly!

Now let's see how we can apply these operators on some operands (a.k.a. arguments) and start doing something interesting with our Scheme calculator.

To apply an operator on some operands we need a pair of parentheses that enclose both the operator and the operands, in order.

    > (+ 3 5)
    8

The operator is always the first thing in the parentheses, followed by the operands. Here + is the operator, 3 is the first operand, and 5 the second operand. The order of the operands is important:

    > (- 13 7)
    6

    > (- 7 13)
    -6

Whenever you see the "parentheses-notation" in Scheme you should immediately recognize that it is the application of an operator to several operands, and you should be able to recognize that the first thing between the parentheses is the operator, the second thing is the first operand, the third is the second operand, etc.

So now we have a simple calculator where we can do one operation after the other. To calculate 3*2 + 5*3 we can type:

    > (* 3 2)
    6

    > (* 5 3)
    15

    > (+ 6 15)
    21

Remember that all of the above are expressions. Each one is being evaluated by DrScheme and a result is returned in its place. Having this in mind we can build more complex expressions, and make our calculator compute 3*2 + 5*3 writing just one big expression:

    > (+ (* 3 2) (* 5 3))
    21

Q: What is the order of evaluation in complex expressions?

When things get too complicated use indentation to make the expression more readable:

    > (+ (+ (- 20 5)
            (+ 10 4))
         (* (- 100 93)
            (* 3.5 
               (- 5 3))))
    579.0

We now know how to use scheme as a decent calculator to do arithmetic. But let's not stop there. Let's see how we can also do Logical calculations.

Scheme has some more primitive expressions, the set of booleans:

    ; True
    > #t
    #t

    ; False
    > #f
    #f

It also provides operators that can be applied on booleans

    ; and : Boolean * Boolean --> Boolean
    ; Logic conjunction

    ; or : Boolean * Boolean --> Boolean
    ; Logic disjunction (Inclusive)

    ; not : Boolean --> Boolean
    ; Logic negation


    > (not #f)
    #t

    > (and #t #f)
    #f

    > (or (and #t
               (or #t #f))
          (or (not #t)
              (not (and (not #f)
                        #t))))
    #t

There are also operators that connect the "world" of numbers and the "world" of booleans. These operators perform tests on numeric data and return a boolean value. These are called predicates.

    ; = : Number * Number --> Boolean
    ; Tests two numbers for equality

    ; < : Number * Number --> Boolean
    ; Tests if the first operand is less than the second

    ; > : Number * Number --> Boolean
    ; Tests if the first operand is greater than the second

    ; <= : Number * Number --> Boolean
    ; Tests if the first operand is less or equal than the second

    ; >= : Number * Number --> Boolean
    ; Tests if the first operand is greater or equal than the second

So for example:

    > (< 300.0001 300)
    #f

    > (= (+ (* 3 50)
            (* 3 25))
         (* 3
            (+ 50 25)))
    #t

Q: What will this return?

    > (< 3 (< 2 1))

Be careful of the contracts of operators to avoid these type errors.

Conditional

There are times that we need the value of an expression to change depending on some condition. Scheme provides a construct to implement this kind of branching.

    (cond 
      (test-1 expr-1)
      (test-2 expr-2)
      (test-3 expr-3)
      ...
      (else expr-n))

The cond is a multi-branch conditional. Each clause has a test and an associated action. The first test that succeeds triggers its associated action. The final else clause is chosen if no other test succeeded.

For example:

      > (cond 
          ((< (sqrt 5) (/ 5 2)) #t)
          (else #f)))

Defining Procedures

At this point our DrScheme calculator can do a great deal of things. It's almost like a scientific calculator, but we are not there just yet. It would be nice if we were able to define our own operators on numbers and booleans and extend the functionality of our calculator. Scheme has a special syntax for doing just that:

    (define (op-name arg-1 arg-2 ...) expr)

With this syntax we can define a new operator called op-name that takes a number of arguments arg-1, arg-2, etc., and when applied evaluates the expression expr and returns the result. expr can refer to the arguments, to produce its resulting value. For example let's define the Boolean operation 'nand', using 'and' and 'not':

    ; nand : Boolean * Boolean --> Boolean
    ; Takes two arguments and returns their negative conjuction
    (define (nand x y)
      (not (and x y)))

We can use our addition just like any other operator:

    > (nand #t #t)
    #f

Let's also define a procedure that computes the average of two numbers:

    ; average : Number * Number --> Number
    ; Returns the average of its arguments
    ; usage:
    ; (average 3 5)    =>  4
    ; (average -7 7)  =>  0

    (define (average x y)
      (/ (+ x y) 2))

Let's also define abs using cond:

    (define (abs x)
      (cond 
        ((< x 0) (- 0 x))
        (else x)))

    ; f->c : Number --> Number
    ; Takes a temperature in degrees Fahreneigh as an argument, and
    ; converts it to degrees Celcius.
    ; Usage:
    ; (f->c 32)  => 0
    ; (f->c 100) => 37.77777777777778

    ; tip : Number * Number --> Number
    ; Takes as arguments the amount of the bill in dollars and the
    ; percentage of tip, and returns the amount of the tip in
    ; dollars.
    ; Usage:
    ; (tip 10 0.15)  => 1.5
    ; (tip 20 0.17)  => 3.4

Ex6: One of the solutions of the quadratic equation is given by the formula:

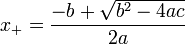
Write the contract, purpose statement, examples, and definition of a procedure quadradic-root that takes as arguments a, b, and c, and computes the root of the corresponding quadratic equation.

    ; circumference : Number --> Number
    ; Takes as an argument the radius r of a circle and computes
    ; its circumference, using the formula 2 * 3.1415 * r.
    ; Usage:
    ; (circumference 1)  =>  9.4245
    ; (circumference 0)  =>  0

Complex Data Types: Pairs

Number and Boolean are primitive data types in Scheme. It is often useful to have more complex data types. Scheme provides such a data type called Pair.

    ; Pair is
    ;    (cons Any Any)

This is a data type definition that tells us how we can create Pairs. It is an abbreviation of writing down the full definitions of the constructor(s):

• Constructor:

  ; cons : Any * Any --> Pair
  ; Takes two arguments of any type and returns a Pair that
  ; contains them
  ; Usage:
  ; (cons 1 3)  =>  (cons 1 3)
  ; (cons 5 #f) =>  (cons 5 #f)
  

In this case a Pair has exactly one choice: to be the result of applying cons to two numbers. (We will see further down that other data types may have more that one ways to construct objects.)

To be able to use Pairs in our programs, Scheme, besides the constructor, provides us with the following:

• Accessors: procedures that return the data stored in a Pair:

  ; car : Pair --> Any
  ; Takes a pair as an argument and returns the datum stored in
  ; the first position of the pair.
  ; Usage:
  ; (car (cons 1 3))  => 1
  ; (car (cons 5 #f)) => 5
  
  
  ; cdr : Pair --> Any
  ; Takes a pair as an argument and returns the datum stored in
  ; the second position of the pair.
  ; Usage:
  ; (cdr (cons 1 3))  => 3
  ; (cdr (cons 5 #f)) => #f
  

• Predicate: a predicate that distinguishes pairs from members of other data types

  ; pair? : Any --> Boolean
  ; Returns #t if its sole argument is a member of the Pair
  ; data type, and #f otherwise.
  ; Usage:
  ; (pair? (cons 1 3))  => #t
  ; (pair? (cons 5 #f)) => #t
  ; (pair? 100)         => #f
  

Let's construct some pairs and get their elements:

    > (define pair-1 (cons 1 2))

    > (define pair-2 (cons #t #f))

    > (car pair-1)
    1

    > (cdr pair-2)
    #f

    > (car (cons #f 3))
    #f

Q: What will be the result of the following?

   > (car (cdr (cons pair-1 pair-2)))

We can define our own complex data types by providing the same three things; constructors, accessors, and predicates.

Let's say that we want to represent points in a two-dimensional space. Each point should have an X and a Y coordinate which are numbers.

    ; Point is
    ;     (cons Number Number)
    ;
    ; The first element of Point is the X coordinate
    ; The second element of Point is the Y coordinate

This data-type definition tells us that Points have the same constructor as pairs, but they only store numbers. The first number represents the X coordinate of the Point, and the second the Y coordinate. We can reuse the same constructors, accessors, and predicates, as Pairs, but we need to make sure that we write down the new meaning that we have given them:

• Constructor:

  ; cons : Number * Number --> Point
  ; Takes two numbers and returns a Point, such that the first
  ; number is the X coordinate of the Point, and the second
  ; number is the Y coordinate of the Point.
  ; Usage:
  ; (cons 1 3)  =>  (cons 1 3)
  ; (cons 5 -2) =>  (cons 5 -2)
  

• Accessors:

  ; car : Point --> Number
  ; Takes a point as an argument and returns its X coordinate.
  ; Usage:
  ; (car (cons 1 3))  => 1
  ; (car (cons 5 -2)) => 5
  
  
  ; cdr : Point --> Number
  ; Takes a point as an argument and returns its Y coordinate.
  ; Usage:
  ; (cdr (cons 1 3))  => 3
  ; (cdr (cons 5 -2)) => -2
  

• Predicate:

  ; point? : Any --> Boolean
  ; Returns #t if its sole argument is a member of the Point
  ; data type, and #f otherwise.
  ; Usage:
  ; (point? (cons 1 3))   => #t
  ; (point? (cons 5 -2))  => #t
  ; (point? (cons #f -2)) => #f
  ; (point? 100)          => #f
  

Now let's use our Points. We can construct Points:

    > (define point-1 (cons 100 10))

    > (define point-2 (cons -20 15))

find out their coordinates:

    > (car point-1)
    100

    > (cdr point-2)
    15

We can also define interesting procedures that manipulate points:

    ; distance : Point * Point --> Number
    ; Takes two points as arguments and computes their distance in
    ; a two-dimensional space.
    ; Usage:
    ; (distance point-1 point-2) => 120.10412149464314
    (define (distance p1 p2)
      (sqrt (+ (sq (- (car p1) (car p2)))
               (sq (- (cdr p1) (cdr p2))))))

    > (distance (cons -2 -3)
                (cons -4 4))
    7.280109889280518

    ; Circle is
    ;     (cons Point Number)

Inductive Data Types: Lists

The data types we have seen so far describe structures that contain a fixed number of elements. Numbers and Booleans contain just one element, their value. Pairs and Points contain 2 elements, the X and Y coordinate. We can say that Circles contain 2 elements, a Point and a Number, or if we expand the definition of Point, we can say that Circles contain 3 elements. In all of these data types we have a fixed number of elements.

There are times that we need data types that can contain an arbitrary number of elements. An example of such a data type is a list of numbers. When we define the List-of-Number data type, we can't decide how many numbers will be in a list at any given time. Such a list may have zero, one, two, etc. elements. In order to define such a data structure we use induction:

    ; List-of-Number is one of
    ;       '()
    ;       (cons Number List-of-Number)

Here we have two ways to create lists---two constructors. Let's start with the second constructor: it gives us a way to create a list with a number in the first position (head) and another List-of-Number as the rest of the list (tail). Notice that we use List-of-Number in the definition of List-of-Number, creating in this way a recursive data type.

Having just the cons constructor is not enough for two reasons: first because it describes lists with at least one element, and second because by itself it describes only infinite lists. That is why we need the first constructor that gives us the empty list, and a way to terminate the constructions of our lists.

We call the first constructor the base case of our inductive data type, and the second the inductive case.

• Constructors:

  ; '() : Nothing --> List-of-Number
  ; creates an empty List-of-Number.
  ; Usage:
  ; '()  =>  '()
  
  
  ; cons : Any * List-of-Number --> List-of-Number
  ; Takes an argument of Any type, and a List-of-Number, and
  ; returns a list that has the first argument as the head of
  ; the list and the second as the tail of the list.
  ; Usage:
  ; (cons 1 '())                   => (cons 1 '())
  ; (cons 1 (cons 2 (cons 3 '()))) => (cons 1 (cons 2 (cons 3 '())))
  

Notice that the List-of-Number and Pair share the cons constructor, just like Pair and Point share the same constructor.

To be able to retrieve the elements in a list, we also need accessors. The empty list doesn't contain any elements, so we don't need any accessor for empty lists. A non-empty list though contains two things, a head element and a tail list, thus we need two accessors for this case:

• Accessors:

  ; car : List-of-Number --> Any
  ; Takes a List-of-Number and returns the element in the head of the List
  ; Usage:
  ; (car (cons 1 '()))                  => 1
  ; (car (cons 1 (cons 2 (cons 3 '()))) => 1
  ; (car '())                           => error
  
  
  ; cdr : List-of-Number --> List-of-Number
  ; Takes a List-of-Number and returns the tail of the List
  ; Usage:
  ; (cdr (cons 1 '()))                   => '()
  ; (cdr (cons 1 (cons 2 (cons 3 '())))) => (cons 2 (cons 3 '()))
  ; (cdr '())                            => error
  

We will need several predicates for lists. First a predicate to distinguish a List-of-Number from other data types, such as Points. Then we will need two more predicates to distinguish the two possible choices of lists: empty lists and non-empty lists:

• Predicates:

  ; list? : Any --> Boolean
  ; Returns #t if its sole argument is a member of the
  ; List-of-Number data type, and #f otherwise.
  ; Usage:
  ; (list? '())          => #t
  ; (list? (cons 1 '())) => #t
  ; (list? 5)            => #f
  
  
  ; null? : Any --> Boolean
  ; Returns #t if its sole argument is the empty List-of-Number
  ; and #f otherwise.
  ; Usage:
  ; (null? '())          => #t
  ; (null? (cons 1 '())) => #f
  ; (null? 5)            => #f
  
  
  ; pair? : Any --> Boolean
  ; Returns #t if its sole argument is a non-empty
  ; List-of-Number and #f otherwise.
  ; Usage:
  ; (pair? '())          => #f
  ; (pair? (cons 1 '())) => #t
  ; (pair? 5)            => #f
  

Let's use the above to experiment with lists:

    > (define list-1 (cons 3 (cons 2 (cons 1 '()))))

    > (car list-1)
    3

    > (car (cdr list-1))
    2

    > (car (cdr (cdr list-1)))
    1

When we want to write a procedure that traverses a List-of-Number given as an argument, we always need to write our procedure using induction, just as we used induction to define the List-of-Number data type. We need a base case to handle the empty list, and an inductive case to handle a list with a head and a tail. For example let's say that we want to write a procedure that can count the length of a list, given as its argument.

    ; length : List-of-Number --> Number
    ; Takes a List as an argument, traverses it, and returns the
    ; number of elements it contains.
    ; Usage:
    ; (length '())                                     => 0
    ; (length (cons 1 '()))                            => 1
    ; (length (cons 1 (cons 3 (cons 5 (cons 7 '()))))) => 4

    (define (length lst)
      (cond 
        ((null? lst) 0)                           ; Base case
        (else (+ 1 (length (cdr lst))))))         ; Inductive case

In the above procedure we use the predicates null? and pair? to distinguish the two possible cases of the structure of lst. If lst is empty, then the list we were given contains no elements, thus the procedure returns zero. If lst is a pair of a number in the head of the list and another List-of-Number in the tail, then the number of elements in lst is one more that the number of elements in the tail of lst. Thus in this case the procedure returns 1 + the result of applying the same procedure to the tail of the list. This is called a recursive application.

Notice here that the recursive application of length is on a smaller list, something that guarantees that eventually length is going to be applied on the empty list, and the recursion will finish (this is why we call this an induction).

We can test our procedure and see what it does work as we want:

    > (length '())
    0

    > (length (cons 5 '()))
    1

    > (length (cons 5 (cons 7 (cons 11 (cons 13 '())))))
    4

Now let's see a procedure that consumes a List-of-Number and produces another. We will define inc-list that increases all the elements of a list by one.

    ; inc-list : List-of-Numbers --> List-of-Numbers
    ; Takes a List-of-Numbers, and produces another list that has
    ; the elements of its input list increased by one.
    ; Usage:
    ; (inc-list '()) => '()
    ; (inc-list (cons 1 (cons 3 (cons 5 (cons 7 '())))))
    ;       => (cons 2 (cons 4 (cons 6 (cons 8 '()))))

    (define (inc-list lst)
      (cond 
        ((null? lst) '())
        (else (cons (+ 1 (car lst))
                    (inc-list (cdr lst))))))

Again here we wrote the procedure in an inductive style. We distinguished between the base case (empty list) and the inductive case (non-empty list). The base case returns an empty list (since there is no number to increase). The inductive case should return a list that has as a head the head of the input list increased by one, and as a tail the result of applying inc-list to the rest of the list (which will increase the rest of the numbers in the list).

Notice that the above two procedures look very similar. In fact we can always derive a template of a procedure that traverses a structure, by just looking at the data type of the structure. For lists we have:

    ; List-of-Number                        ;  f : List-of-Number --> ...
    ;                                       ;  (define (f lst)  
    ;  is one of                            ;    (cond
    ;       '()                             ;      [(null? lst) ... ]
    ;       (cons                           ;      [else        ...
    ;         Number                        ;                   ... (car lst) ...
    ;         List-of-Number)               ;                   ... (f (cdr lst)) ...]))

Therefore, to define any procedure f that works on the data type List-of-Number we need to take an argument of that data type. Then, because there are two cases of List-of-Number (empty and non-empty), we need a conditional branch in our procedure to discriminate between the two. In the case of '() there are no elements to extract from the list, thus we do something depending on the functionality of f. In the case of (cons Number List-of-Number) there are two elements to extract from the list. A Number (by using car), and another List-of-Number (by using cdr). We can use the Number in the way that the algorithm of f requires. To process the List-of-Number part we always apply the same procedure f.

    ; inc-list-p : List-of-Number --> List-of-Number
    ; Takes a List-of-Number as its argument, and produces another
    ; List-of-Number that has the same elements as the input List, except that
    ; all elements greater than zero are increased by one.
    ; Usage:
    ; (inc-list-p '()) => '()
    ; (inc-list-p (cons 1 (cons 3 (cons 5 (cons 7 '())))))
    ;       => (cons 2 (cons 4 (cons 6 (cons 8 '()))))
    ; (inc-list-p (cons 1 (cons -1 (cons 0 '()))))
    ;       => (cons 2 (cons -1 (cons 0 '())))