Chapter 3.

1.

On a square sheet of graph paper ( with 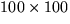little squares ) I have drawn several rectangles. Each rectangle consist of entire little squares of the grid, different rectangles never overlap or touch each other (see Fig. 2).

Given the array A[100][100] in which an entry A[i][j] = 1 if the square (i, j) of the grid belongs to one of the rectangles, and A[i][j] = 0 otherwise. Write a program that counts the number of rectangles. (Think of this as the easiest problem related to "computer vision".)

2.

Print out in the increasing order all simple fractions between and 1 such that their denominators are no greater than 7.

Example: 3/6 should not be printed, because, although its denominator is less than 7, it is not simple and can be further simplified, 3/ 6 = 1/2.

3.

Given an array of positive integers A[N] and an integer M . It is known that the sum of several elements of the array is equal to M . Neither their positions nor their number are known. Find them.

Notes: 1. Notice that the elements need not be consequtive. For instance, for

and M = 17 we have 8+4+5 = 17.

2. You may want to solve a simplified version of the problem, assume first that the number of desired elements is also given (say, 3, as in the above example).

3. Try to solve the problem without the condition that all inetgers in the array are positive.

4.

Given an inetger array A[N] of length N. Rearrange its entries so that all the non-zero entries are in the beginning of the array (and their original relative order is preserved), and all the zeros are at the and of the array. You are not allowed to use another array.

5.

Given a two-dimensional arrray A[M][N]. We call an entry of the array a saddle point if it is both the smallest one in its row and the largest one in its column. Output the indices of a saddle point of A or signal failure if no such entry exists.

6.

Given two integer arrays X[N] and Y[M], N > M. Write a program that determines if the first array X[N]contains a subsequence of M entries same as those of Y[M], in the same order and outputs either 'yes' or 'no'.