CS3800 09F: Homework 03

Assigned: Wed 30 Sep 2009
Due: Wed 07 Oct 2009

General Instructions

1. Please review the grading policy outlined in the course information page.

2. On the first page of each part of your solution write-up, you must make explicit which problems are to be graded for "regular credit", which problems are to be graded for "extra credit", and which problems you did not attempt. Please use a table something like the following

   Problem	01	02	03	04	05	06	07	08	09	...
   Credit	RC	RC	RC	EC	RC	RC	NA	RC	RC	...

   where "RC" is "regular credit", "EC" is "extra credit", and "NA" is "not applicable" (not attempted). Failure to do so will result in an arbitrary set of problems being graded for regular credit, no problems being graded for extra credit, and a five percent penalty assessment.

3. You must also write down with whom you worked on the assignment. If this changes from problem to problem, then you should write down this information separately with each problem.

Problems

Required: 6 of the following 8 problems
Points: 16 pts per problem

1. Convert the following finite automata to regular expressions:
   • the DFA from Figure 1.4, pg. 34
   • machine M₁ from Exercise 1.1.

2. Convert the following finite automata to regular expressions:
   • the NFA from Exercise 1.16, part (a)
   • machine M₂ from Exercise 1.1.

3. Exercise 1.22, part (b)

4. Problem 1.31. (Hint: Think about what it means to run a finite automata backwards.)

5. Problem 1.32.

6. Problem 1.35. (Hint: See Problem 1.50 and its solution on pg. 97 for ideas. You do not need the Pumping Lemma.)

7. Problem 1.39. Clearly state your language A_k.

8. Given any two sets A and B, the set difference A-B is constructed by removing the elements in B from A. For example, if A = {1, 2, 3, 4, 5} and B = {2, 4, 6, 8}, then A-B = {1, 3, 5}. In mathematical terms,

   

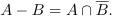
   Let R be any regular language and let N be any non-regular language. (Note: R is not the set of regular languages; it is a variable which represents any particular regular language. Similarly for N.)

   For each of the following assertions, either prove that the assertion is true or demonstrate that it is false by providing a counterexample.

   • R-N is always regular.
   • N-R is always non-regular.

Switch to:

• Homework 02
• Homework 04