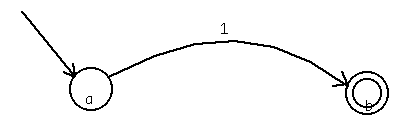
Here we exhibit some of the aspects of parsing the simple finite-state diagram below. The diagram arrows are simply drawn as a line or curve and two straight lines near the point, forming the arrowhead. The exact positioning, angles, and lengths of the arrowheads is not crucial to the analysis. The positioning of the three labels is not critical either. The full finite-state automata grammar is available for perusing. It may help clarify some of the details of the parsing whose results are illustrated below. Installation of the diagram in the pyramid required about 700 msec and parsing required about 250 msec. (This is relatively slow, given the simplicity of the diagram, but this is because the installation and parsing of circles is not well optimized.)

The grammar for finite-state automata uses existentially quantified variables and negation in the discovery of the start states. They must have an incoming arrow which itself has no other state touching its tail. This is specified in the rule below:

   ( Init-state -> A-state  Arrow
     (A-state)
     (Arrow  (touch A-state '?)
      :constraints  (touch (reach-pt Arrow) A-state) 
                    (null (some* [a-state] :in (touch '? (leave-pt Arrow))))))

The top-level production has three constituents:

FA -> Init-state Transitions Final-states

Perhaps the most interesting thing about the grammar is that the three constituents share various elements. They do this so they can identify structures correctly by their relations to others, by their geometrical context. This is most easily seen in the three images below, which show the highlighted objects in the three top-level constituents.

Figure 1. Highlighted elements of the Init-state. Both the state-circle and the incoming arrow without any tail object are used to determine that "a" is the initial state.

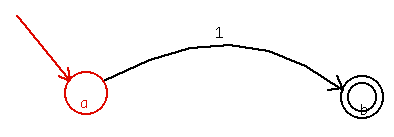
Figure 2. Highlighted elements of the Transitions (there is only one). Note that the circle in the initial state show in Fig. 1 is used again (shared) in defining the transition. Each state circle in a large diagram is a participant in all the transition objects that leave or enter that state. Because each entity such as a state is treated as a unique object, and installed in the pyramid, they are not recreated each time they are used in a distinct constituent parse.

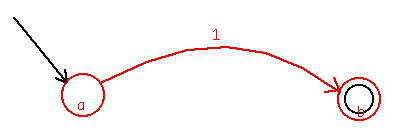
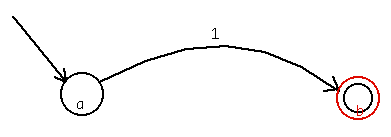
Figure 3. Highlighted elements of the Final-states (there is only one). A final state is distinguished by having one circle contained in another. Here the end-state of the transition highlighted in Fig. 2 is reused in the final state.

		Next: Gene Diagrams

		Back to Index page