Mathematical Images for Tanabata

The images generated by math4Tanabata2.html are inspired by the Tanabata legend. The drawing canvas is treated as a piece of the complex plane with 0 + 0 i at the center. Each point, z is lined up with a target point T = x + y i. The point z is then sent on a journey through its powers zⁿ until a power, zⁿ lines up again, as close as possible with T and z. The value of n is used to determine the color assigned to the point z.

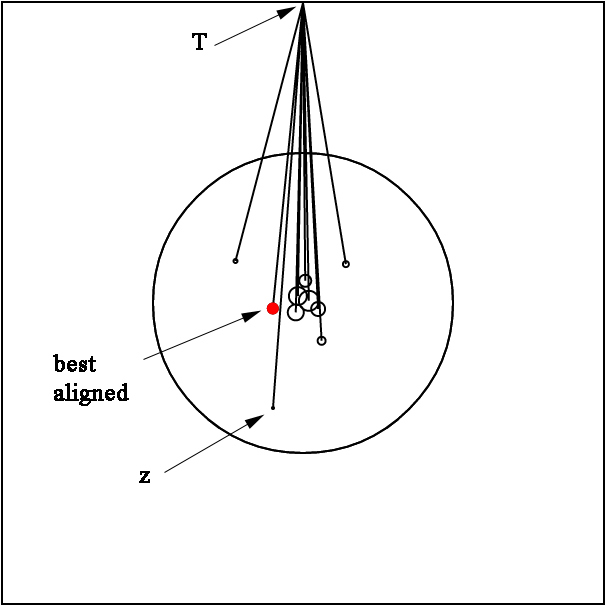
The point z and its powers z² through z¹⁰ are shown with circles of increasing diameter along with lines to the target point T. The point z⁵ lines up best with z and T so the integer 5 wil be used to set a color for z.

The "best alignment" is determined in one of two ways:

If epsilon > 0: n is the smallest integer less than or equal to N such that the slopes of the line segments from z to T and from zⁿ to T differ by less than epsilon or N if they never get that close.
If epsilon = 0: n is the integer between 2 and N that gives the closest slopes.

Once n is computed, t = n/N is used to blend color A and color B to give:
color(z) = t*colorA + (1-t)*colorB where red, green, and blue are blended separately.

The gradient color is chosen to be white minus the average of colorA and colorB. There are some choices you can make about how the gradient color is to be used. The small green arrows indicate the direction in which the gradient color gets brighter. You can also use the "mod" buttons to suppress the Red, Green, or Blue components of the gradient for every second, third, or fifth value of n. Varying these choices can add more color variation and a sense of depth to the image.

The width is the mathematical width of the drawing canvas. If the width is set to 2, values of x and y will run from -1 to +1.

"Save drawing" will open a a new tab in your browser with a png of your image that you can save to disk.