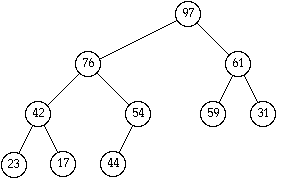
1 The following array of current size 10 represents a heap structure:

1	2	3	4	5	6	7	8	9	10	11
97	76	61	42	54	59	31	23	17	44

The tree diagram of this heap is shown below:


a. (5 points) Insert a new value 86 into the heap. Draw the new heap when done. [Increase the heap size from 10 to 11 place 86 initially into slot 12 of the array, then perform upheap to restore the heap conditions.] Show the resulting array.

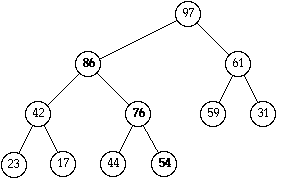
1	2	3	4	5	6	7	8	9	10	11
97	86	61	42	76	59	31	23	17	44	54

b. (10 points) Start again with the original heap of 10 elements. Show the result after each swap of two passes of HEAPSORT. Note: After one pass 97 is in position 10 and the values in positions 1 .. 9 again form a heap.
You may have extra space.

1	2	3	4	5	6	7	8	9	10
97	76	61	42	54	59	31	23	17	44
44	76	61	42	54	59	31	23	17	97	97 swapped into place
76	44	61	42	54	59	31	23	17	97
76	54	61	42	44	59	31	23	17	97
76	54	61	42	44	59	31	23	17	97	pass one finished
17	54	61	42	44	59	31	23	76	97	76 swapped into place
61	54	17	42	44	59	31	23	76	97
61	54	59	42	44	17	31	23	76	97	pass two finished

Bold entries are no longer part of the heap.

2. (5 points) Write a recursive function

int CountRange(Node* root, int low, int high);

int CountRange(Node* root, int low, int high){
	if (low > high) return 0; // or precondition: low <= high
	if (!root) return 0;
	if (root->data > high) return CountRange(t->left,  low, high);
	if (root->data <  low) return CountRange(t->right, low, high);
	// if you got this far, low <= root->data <= high
	return 1 + CountRange(t->left, low, high) + CountRange(t->right, low, high);
}

Last Updated: May 26, 1997 10:06 pm by