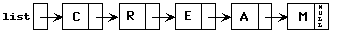
Node* & D(Node* &  list){
	if (list){  
		Node * p;
		p = new Node;
		p->data = list>data;
		p->next = D(list->next);
		list->next = p;
	}
	return list;  
}

2. (5 points) Show the output when a call is made to H(4).

void H(int N){
	cout << N << endl;
	if (N > 1) {
		H(N-1);
		H(N-2);
	} 
}

output  nesting
4   	H(4)
3  	   H(3)
2  	     H(2)
1  	       H(1)
0  	       H(0)
1  	     H(1)
2  	   H(2)
1  	     H(1)
0  	     H(0)

cout << "K(4) = " << K(4) << endl;
cout << endl;
cout << "K(3) = " << K(3) << endl;

int K(int N){
	static int count = 1;
	cout << setw(8) << count++ << setw(8) << N << endl;
	if (N == 0) return 1;
	if (N == 1) return 1;
	return K(N-1) + K(N/2);
}
output     	nesting
1       4      K(4) returns 5
2       2         K(2) returns 2
3       1          	K(1) returns 1
4       1          	K(1) returns 1
5       3         K(3) returns 3
6       1          	K(1) returns 1
7       2          	K(2) returns 2
8       1           		K(1) returns 1
9       1           		K(1) returns 1
K(4) = 5



10      3      K(3) returns 3
11      1         K(1) returns 1
12      2         K(2) returns 2
13      1          	K(1) returns 1
14      1          	K(1) returns 1
K(3) = 3

int Q(int A[], int size)

int Q(int A[], int size){
// size > 0
	if (size == 1) return A[0];
	int x = Q(A, size-1);
	if (x > A[0]) return x;
	return A[size - 1];
}

Last Updated: April 27, 1997 10:15 pm by