Goals:

This assignment is designed to illustrate and practice several important ideas of computer science. The first is the practice of implementing functions that call themselves recursively - in a non-trivial manner. The second is to learn a little bit about the use of formal grammars and rewriting systems for defining a language or a formal system. In addition, you will use again some of the plotting tools (namely the ScalingTransform) introduced earlier. You will also have to focus on correct use of arguments in function definitions and calls - especially the pointers to character strings.

Tutorial:

A formal grammar is a system built of a finite sets of symbols (the alphabet) and a finite set of rules that defines what types of words or sentences (strings of characters from the alphabet) are allowed in this language. The idea is similar to written languages - there we have rules for constructing sentences using different types of words (parts of speech).

The grammars we will look at are called L-systems (or Lindenmayer systems) - and we will only look at the simplest of these - namely the L-systems based on edge rewriting rules. The alphabet we will use describes how to create a drawing from a series straight line segments. We have supplied a page of assorted Fractal Grammars.

We illustrate the basic idea by looking at one of the most famous fractal curves that is based on edge rewriting - the Koch snowflake. The alphabet for Koch snowflake has only four symbols:
S which is a rule for the initial drawing
F which means to move forward a fixed distance
+ which means to turn right 60
- which means to turn left 60

The grammar for Koch snowflake can then be described by the following two rules:
S -> F++F++F
F -> F-F++F-F

Exercise:
Draw for yourself the first level of the curve - the one described by the rule S . You should get an equilateral triangle. Now replace each side (in the direction in which you were drawing them - so that the meaning of the left and right is preserved) using the rule F . The resulting figure should be a six-sided star. Continue by replacing each side one more time. You can also run the application to see the next one or two levels of recursion. A picture is shown below, but you should do the drawing to see how the drawing is constructed.

Koch Snowflake: Recursion levels 1 through 6

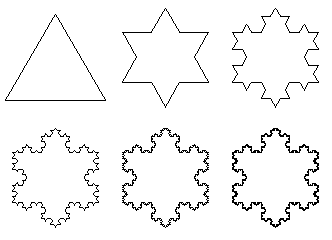
Sometimes, we may need to distinguish between two types of lines - we may think of them as a right and left line - or one which grows on the right and one which grows on the left. In that case we need two new symbols in our alphabet - we will call them L and R . Finally, in some curves, we want to move ahead without drawing a line. This will be represented by symbol f .

Exercise:
Experiment with some of the curves that use the L-rule or the R-rule and see how they behave. Try to draw the first three levels of the Sierpinski Gasket to understand how it fills the three triangles.

The assignment:

The lines are drawn by a LOGO-like Turtle. The class Turtle records its current position as a Point2D p , its direction (or angle) as a double a , and the step size or distance as a double d . The drawing is accomplished by the following commands (functions):

t.Forward( ) turtle draws a line starting at its current position p; it travels the distance d in the direction given by a

t.Skip( ) the turtle moves the same way as above, but does not draw anything

t.Right(angle) turtle turns angle degrees to the right

t.Left(angle) turtle turns angle degrees to the left

It is possible to move the turtle ahead more than one step (or even half a step) but we will not need this feature for our assignment.

You are responsible for defining the class Grammar that will record the rewriting rules and perform the actions defined by the rules. Your file Grammar.h should contain the complete declaration and definition of the class Grammar.

The member data of this class are five character strings (defined as LargeBuffer type) that will contain the rules for S , F , R , L , and f . In addition, the grammar needs to record the angle by which we turn. Later, we may need a couple of boolean variables to mark whether we want to print all moves, and whether we want to scale the drawing.

The class Grammar should have the following member functions:

ReadGrammar( ) that will read in the five rules and the turning angle

ShowGrammar( ) that will print out the strings, if the user so chooses

Fmove(...) that will perform the next step in the drawing

DrawCurve(...) that will be called from the main to start the drawing process.

Explanation of the drawing functions:

DrawCurve just calls Fmove, passing to it the following arguments:
the number n of recursive levels we wish to draw.
char *S
the turtle (by reference)


Fmove loops through the string that was passed to it as argument, initiating an action for each character c according to the following rules:


If the recursion level is 1 - the lowest level and the character c is:

letter F, R, or L: turtle calls Forward( )
letter f turtle calls Skip( )
letter + or - turtle turns right or left by a given angle a

If the recursion level is greater than one and the character c is:


letter F: turtle calls Fmove with recursive level (n-1) and pointer to grammar string F again, passing the turtle by reference

letter R: turtle calls Fmove with recursive level (n-1) and pointer to grammar string R again, passing the turtle by reference

letter L: turtle calls Fmove with recursive level (n-1) and pointer to grammar string L again, passing the turtle by reference

letter f: turtle calls Fmove with recursive level (n-1) and pointer to grammar string f again, passing the turtle by reference

letter + or - turtle turns left or right by a given angle a

You may want to print each move as it is made, so that you know what is going on. However, for some drawings this generates an exorbitant amount of output.

Exercise:
Show in a table of the number of moves for each level of recursion n for the Koch snowflake (with n going from 1 to 6).

Exercise:
Draw the first three levels of the Dragon curve.

Part 2:

The application FractalRecursion allows you to scale the drawing so it would fit within any bounds. The scaling is done using the same ScalingTransform class you have used earlier. The idea is to compute the bounding rectangle for the drawing, using the real world coordinates, then compute the scale factor and the shift needed to center the drawing within the designated rectangle in the Drawing Window.

To allow scaling, the Turtle class contains as its member data a ScalingTransform object s, and a Rect2D object called bounds. To implement the scaling, you need to do the following:

Write a helping function AdjustBounds(...) that will take two arguments - the current turtle position and the bounds rectangle. If the turtle is not positioned within the bounds rectangle, it will increase the rectangle in the appropriate directions.

Add a bool field to the arguments for the Fmove(...), to indicate whether you are just computing the bounds or actually drawing the picture

Modify the Fmove(...) function, so that it calls Skip instead of Move when computing the bounds. It also calls AdjustBounds( ) to adjust the size of the bounds rectangle as needed.

Add a new function ScaleCurve(...) to the class Grammar. The function receives the same arguments as DrawCurve, and an additional argument - the target rectangle in the Drawing Window (type Rect).

This function starts by saving the current turtle position and angle.

Next, it sets the bounds object in the Turtle class to the current turtle position (so you have a rectangle of width and height equal to zero, centered at the current turtle location.

It then calls the function Fmove( ) with the boolean value indicating that we only need to compute the bounds.

Next, the ScalingTransform is set using new bounds and target rectangles.

The turtle position needs to be reset to where it was when we started to compute the scaling

Finally, the function Fmove( ) is called with the boolean value requesting the actual drawing to be done.

Turn in: Source Code - hard copy and diskette, Handwritten exercises and printouts as indicated in this document.

Last Updated: April 20, 1997 10:55 am by