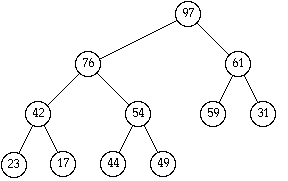
1 The following array of current size 11 represents a heap structure:

1	2	3	4	5	6	7	8	9	10	11	12
97	76	61	42	54	59	31	23	17	44	49

The tree diagram of this heap is shown below:



a. (5 points) Insert a new value 86 into the heap. Draw the new heap when done. [Increase the heap size from 11 to 12, place 86 initially into slot 12 of the array, then perform upheap to restore the heap conditions.]

1	2	3	4	5	6	7	8	9	10	11	12
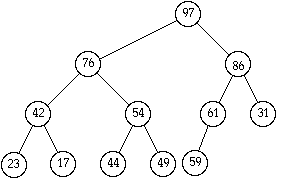
97	76	61	42	54	59	31	23	17	44	49	86
97	76	86	42	54	61	31	23	17	44	49	59

b. (10 points) Start again with the original heap of 11 elements. Show the result of each pass of HEAPSORT. Note: After one pass 97 is in position 11 and the values in positions 1 .. 10 again form a heap.

1	2	3	4	5	6	7	8	9	10	11
97	76	61	42	54	59	31	23	17	44	49
76	54	61	42	49	59	31	23	17	44	97
61	54	59	42	49	44	31	23	17	76	97
59	54	44	42	49	17	31	23	61	76	97
54	49	44	42	23	17	31	59	61	76	97
49	42	44	31	23	17	54	59	61	76	97
44	42	17	31	23	49	54	59	61	76	97
42	31	17	23	44	49	54	59	61	76	97
31	23	17	42	44	49	54	59	61	76	97
23	17	31	42	44	49	54	59	61	76	97
17	23	31	42	44	49	54	59	61	76	97

2. (5 points) Write a C++ function that takes as input a pointer to the root of a binary tree, and prints the node values of the tree in level order. Assume you have available a Queue Class, to build a queue of node pointers, with the following public member functions:

	// default constructor (makes the empty queue)
	Queue ();
	
	// destructor
	~Queue();
	
	// conditionals: empty? full? - DonŐt worry about full.
	bool IsEmpty ();
	
	// add new item to the queue
	Queue& Enqueue (Node* data);
	
	// remove item from the queue
	Node* Dequeue ();
	};


void levelOrder(Node* t){
	Queue Q;
	if (t) Q.Enqueue(t);
	while (!Q.IsEmpty()){
		Node* p = Q.Dequeue();
		cout << P->data << endl;
		if (p->left)  Q.Enqueue(p-left);
		if (p->right) Q.Enqueue(p->right);
	}
}
	

3. (5 points)Write a recursive function

	int PrintRange(Node* root, int low, int high);

int PrintRange(Node* root, int low, int high){
	// This will print the records in order
	if (root){
		datatype d = root->data;
		if ((low < d) && (root->left)) PrintRange(root->left, low, high);
		if ((low <= d) && (d <= high)) cout << root->data << endl;
		if ((d < high) && (root->right)) PrintRange(root->right, low, high);
	}
}

Last Updated: May 26, 1997 9:38 pm by