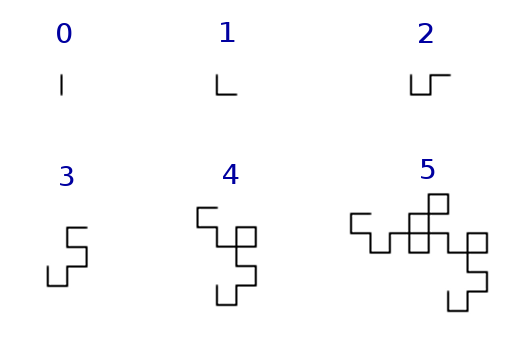
You've probably read about them (accumulators) in the book right? If not have a quick look through it... not too long, because we have a lot of cool stuff to get through.
Accumulator style functions are those that (you guessed it) accumulate knowledge in recursive calls, rather than making "blind" structurally recursive calls (though accumulator style functions can also be, and usually are, structurally recursive).
Example: Here's an implementation of list length in both regular and accumulator style
;; length.reg : [Listof X] -> Number
(define (length.reg lst)
(if (empty? lst) 0
(add1 (length.reg (rest lst)))))
(check-expect (length.reg (list 1 2 3 4 5)) 5)
;; length.acc : [Listof X] -> Number
(define (length.acc lst)
(local [(define (loop lst acc)
(if (empty? lst) acc
(loop (rest lst) (add1 acc))))]
(loop lst 0)))
(check-expect (length.acc (list 1 2 3 4 5)) 5)
Notice that in order to keep the contracts the same, I used a
local recursive function, rather
than adding an argument to the main function.
So it begins...
-
Consider the function
-
Quickly write a "follow the template" recursive
function definition of
sum. -
Now write a second definition of
sumusing DrRacket'sfoldrorfoldlloop function(s). -
Transform your recursive definition
of
suminto an accumulator style function. Hint you need a local helper with an extra argument to "accumulate" the sum-so-far.
sum that sums all the
elements in a [Listof Number].
-
Lets do the same process for the function
-
Quickly write a "follow the template" recursive
function definition of
product. -
Now write a second definition of
productusing DrRacket'sfoldrorfoldlloop function(s). -
Transform your recursive definition of
productinto an accumulator style function.
product
that computes the product of all the elements in
a [Listof Number].
-
Design a function,
absolute->relative, that takes a list ofPosns and converts it into a relative list ofPosns. In a relative list, eachPosnis interpreted relative to the one that came before it, and the firstPosnis interpreted relative to(0,0). In other words, return a new list ofPosns that are adjusted so that they represent the change in position from the previousPosnin the list.Hint: what gets accumulated/remembered between recursive calls? How do you calculate the current element from it?
Here's a few tests...
;; No Posns (nothing interesting) (check-expect (absolute->relative '()) '()) ;; One Posn (still nothing interesting...) (check-expect (absolute->relative (list (make-posn 4 5))) (list (make-posn 4 5))) ;; A bunch of Posns... (check-expect (absolute->relative (list (make-posn 1 6) (make-posn 20 13) (make-posn 5 15) (make-posn 15 5) (make-posn 20 7))) (list (make-posn 1 6) (make-posn 19 7) (make-posn -15 2) (make-posn 10 -10) (make-posn 5 2))) -
Design a function,
relative->absolute, that converts a relative list ofPosns back into a normal list ofPosns.
Note: The two functions you've designed should have no effect when composed:
(define a-lop (list (make-posn 5 7) (make-posn 14 13))) (check-expect (relative->absolute (absolute->relative a-lop)) a-lop)
A bit of fun before we move on...
-
Consider the program below... what does it do? (Hint... run it
and find out)
-
Transform
draw-dotsinto accumulator style. Call the new functiondraw-dots-acc. What does your function accumulate? Use it in thebig-bangto be sure it works right. -
Add a number/label to each dot by designing new
functions,
put-num-dotanddraw-num-dots. Make suredraw-num-dotsis in accumulator style, and use it instead ofdraw-dots-accin thebig-bang. See Image (2) below for an example of what we expect (after a few clicks).Hint: you'll need to
textandnumber->string, but you already guessed that...If your numbers aren't in order, then fix them so they do not change as dots are added. You may need to modify the accumulator's starting value and its update expression.
-
Design the function
draw-lines, in accumulator style that draws lines between the dots. Hint: you'll also want to pass the previous point's coordinates (in addition to the accumulator) when you make your recursive call, since the image functionlinecreates a line from (0,0) to the given x/y. See Image (3) for an example. -
Finally, design the function
draw-num-linesthat draws both lines and number/labels on the dots. See Image (4) for an example. This function doesn't have to be in accumulator style, but if you're working off your other function it probably will be.
(require 2htdp/image)
(require 2htdp/universe)
;; Width and Height of our Scene
(define WIDTH 300)
(define HEIGHT 300)
;; Basic empty scene
(define base-scene (empty-scene WIDTH HEIGHT))
;; A World is a [Listof Posn]
;; put-dot : Scene Posn -> Scene
;; Put a single Dot into the Scene at the given Posn
(define (put-dot scn p)
(place-image (circle 3 "solid" "blue")
(posn-x p) (posn-y p)
scn))
;; draw-dots : World -> Scene
;; Draw the dots of the World (a list of Posn)
(define (draw-dots ps)
(cond [(empty? ps) base-scene]
[else (put-dot (draw-dots (rest ps)) (first ps))]))
;; mouse-click : World Number Number String -> World
;; Add a new Posn to the World if the mouse was clicked
(define (mouse-event w x y what)
(cond [(string=? what "button-down")
(cons (make-posn x y) w)]
[else w]))
(big-bang '()
(to-draw draw-dots)
(on-mouse mouse-event))
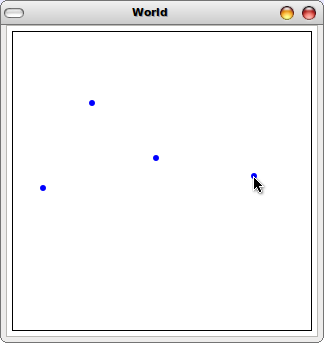 (1) Original |
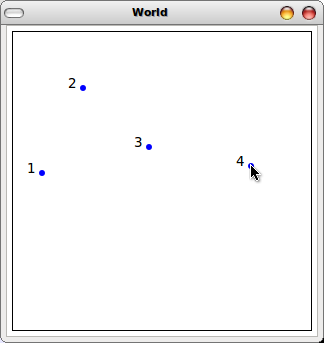 (2) Just numbers |
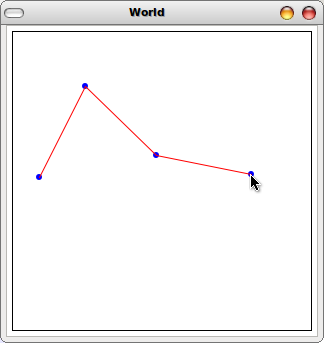 (3) Just lines |
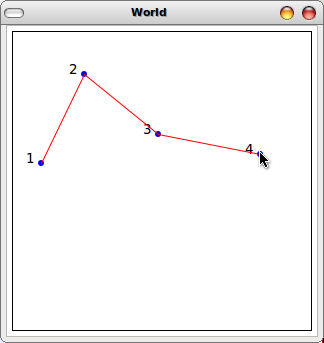 (4) All together |