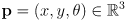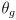Here is one way to modify the above algorithm so that it does not require decrease-key, and so that it does not mutate the sort key of any object that has already been added to the priority queue:
init empty priority queue Q of (vertex, dist) pairs sorted by increasing dist
# the dist part of each pair is immutable; more than one pair can be created for a single vertex
for each vertex v set v.visited = false, v.dist = infinity
set goal.dist = 0
add make-pair(goal, 0) to Q
while Q not empty # O(E) since inner loop adds a pair for every edge
(v, d) = pop Q # O(log E) with binary heap (Java PriorityQueue)
if not v.visited
set v.visited = true
# this inner loop iterates a *total* of O(E) times
for each neighbor vertex n of v with n.visited = false and n.dist > (v.dist + dist(v,n))
set n.next = v, n.dist = v.dist + dist(v,n)
add make-pair(n, n.dist) to Q # O(log E) with binary heap (Java PriorityQueue)
to any goal configuration
sides then it also has
of the polygon vertices, starting at an arbitrary vertex and traveling around the polygon in counterclockwise order if the robot is to remain outside the polygon, or clockwise order if the robot is to remain inside the polygon
(no orientation needed)
of a map as the set of all points in the plane which are not in collision with any obstacle
to any other in the plane (as long as there are no obstacles in the way), it just would always be facing
, make a new virtual obstacle
which is the trace of the robot reference point as the robot “slides around”
and
coordinates are the corresponding parts of the robot pose
and the third “
” coordinate is
groups of free cells into larger free cells
, will it collide with any obstacle in the map?”
are randomly generated
already in the tree closest to that new vertex is found
at its end is added to the graph
, which is the normal of the top and bottom faces of the rect
, which is the normal of the left and right faces of the rect
plus a vector
from
are half the width and half the height of the rect)
plus a vector
from
to one of its end points (i.e. the two endpoints are
)
, so the rect is centered at the origin
and
out from the origin
; the closest this comes to the origin is
by
to get a vector
perpendicular to the segment; this boils down to
is also symmetric about the origin, and extends out at most
are always positive, but
each be positive or negative; reasoning about the four possible sign combinations shows that
comparisons to
to allow segments which are merely tangent to the rect (i.e. that just glancingly touch it) to be considered as not intersecting
where
is the number of edges in the graph
, the algorithm will find a shortest path from every other vertex
to get the distance (edge weight) from vertex
to
is the length of a shortest path from
is minimal; i.e.
then
on the way from
where
is the number of vertices and
time to search for the mimimum distance new vertex at each step. This can be simplified to
since
.
amortized by using a 
in this implementation.
