Problem Set 1
Purpose The purpose of this problem set is to remind you of the pattern-matching skills that your elementary-school teachers tried to teach you and to get you to “play” with BSL and DrRacket.
Finger Exercises Run a program from the HtDP/2e Prologue. Modify it and watch how its behaviors changes. HtDP/2e: exercises 1, 2, 3, 5, 7, 9, 10.
This is the only problem set to be completed without a partner and handed in on paper. Solutions must be submitted to Prof. Van Horn’s office, 350 WVH, before 7PM. You may put it under the door if he is not in.
![]()
Problem 1 An elderly woman suffers from type II diabetes. She injects insulin based on measurements of her blood sugar level. If the blood sugar level is less than 115, she doesn’t need to inject any insulin at all. For a value of 115, she injects 1 unit of insulin. For every additional increase of 20 in her blood sugar level, she gets one additional unit of insulin. (Thus, for a blood-sugar level of 134, she gets 1 unit; for a blood-sugar level of 135, she gets 2 units.)
How much insulin does she need to inject for a blood sugar level of 140? 180?
Make a table that shows the number of units of insulin injected for blood sugar values of 100, 110, 120, ..., 200. Create a formula for calculating the insulin injections. Use the formula to determine how many units of insulin the woman needs to inject for a blood sugar level of 290.
Use DrRacket’s interaction area as a calculator.
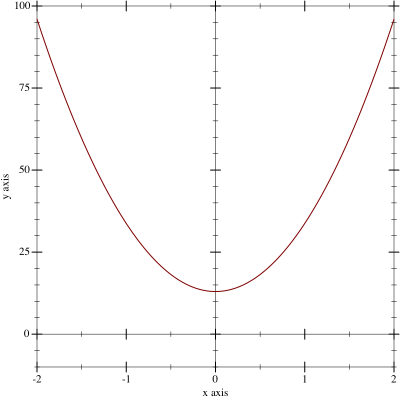
Problem 2 A pool player throws a ball on a pool table, and it then happens to roll along the diagonal. Someone films the action and then measures the balls trip:
after t =
0
1
2
3
4
s
it has traveled d =
13
33.75
96.0
199.75
345.0
cm
Develop a formula that calculates how far the ball gets in t seconds. Check the formula for the first five entries in the above table. If it doesn’t work, work harder. When it works, figure out how far the ball gets in 6s.
New Hint As discussed in class, functions come with many representations: tables, graphs, rules (formula), and so on. Here you are given a (partial) table, and your task is to guess a rule that explains how far the ball gets in t seconds. One way to guess such formulas is to switch representations. Here you could go from a table to a graph:
(+ (* a t t) b)
Use DrRacket’s interaction area as a calculator.
Challenge Canceled for homework The ball lands at (12,5) and happens to travel along the straight line from there to 0,0:
Given the formula, can you figure out the distance the ball travels along the long/short side of the table? Develop a formula.
Recall what sin and cos compute. Try to use those functions to develop a formula.
They pay a base fee of $10 per week just for her to be around if she is needed and $4 per container that needs to be handled.
Use DrRacket’s interaction area as a calculator.
Problem 4 In BSL, you can juxtapose strings just like you can add numbers:
> (string-append "hello" " " "world") "hello world"
Develop the function greeting. It accepts a string and returns a greeting for a formal letter, prefixing the given name with "Dear " and concluding the string with a colon. Thus, (greeting "Prof. Amal") produces "Dear Prof. Amal:" as the result.
Develop the function my-star. It accepts a color string and returns an image of a 5-cornered star of radius 12 of that color. For example, if you apply my-star to "red", it returns the above image.